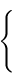Generators selected (1); t(1, 0, 0); t(0, 1, 0); t(0, 0, 1); (2); (3)
Multiplicity, Wyckoff letter,
Site symmetry | Coordinates |
|
| | |
| | (1) x, y, z | (2) -x, -y, z | (3) x, -y + 1/2, z + 1/2 | (4) -x, y + 1/2, z + 1/2 |
|
I Maximal translationengleiche subgroups
| [2] P1c1 (7) | 1; 3 |
| 0, 1/4, 0
|
| [2] Pn11 (7, P1c1) | 1; 4 | b, a, -b - c
|
|
| [2] P112 (3) | 1; 2 |
|
|
II Maximal klassengleiche subgroups
[2] a' = 2a
| Pnn2 (34) | <2; 3 + (1, 0, 0)> | 2a, b, c | |
| Pnn2 (34) | <(2; 3) + (1, 0, 0)> | 2a, b, c | 1/2, 0, 0 |
| Pnc2 (30) | <2; 3> | 2a, b, c | |
| Pnc2 (30) | <3; 2 + (1, 0, 0)> | 2a, b, c | 1/2, 0, 0 |
[3] a' = 3a
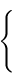 | Pnc2 (30) | <2; 3> | 3a, b, c | | | Pnc2 (30) | <3; 2 + (2, 0, 0)> | 3a, b, c | 1, 0, 0 | | Pnc2 (30) | <3; 2 + (4, 0, 0)> | 3a, b, c | 2, 0, 0 |
|
[3] b' = 3b
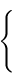 | Pnc2 (30) | <2; 3 + (0, 1, 0)> | a, 3b, c | | | Pnc2 (30) | <2 + (0, 2, 0); 3 + (0, 3, 0)> | a, 3b, c | 0, 1, 0 | | Pnc2 (30) | <2 + (0, 4, 0); 3 + (0, 5, 0)> | a, 3b, c | 0, 2, 0 |
|
[3] c' = 3c
| Pnc2 (30) | <2; 3 + (0, 0, 1)> | a, b, 3c | |
- Series of maximal isomorphic subgroups
[p] a' = pa
| Pnc2 (30) | <3; 2 + (2u, 0, 0)> | pa, b, c | u, 0, 0 | | | p > 2; 0 ≤ u < p
p conjugate subgroups for the prime p |
|
[p] b' = pb
| Pnc2 (30) | <2 + (0, 2u, 0); 3 + (0, p/2 - 1/2 + 2u, 0)> | a, pb, c | 0, u, 0 | | | p > 2; 0 ≤ u < p
p conjugate subgroups for the prime p |
|
[p] c' = pc
| Pnc2 (30) | <2; 3 + (0, 0, p/2 - 1/2)> | a, b, pc | | | | p > 2
no conjugate subgroups |
|
I Minimal translationengleiche supergroups
| [2] Pban (50); [2] Pnna (52); [2] Pmna (53); [2] Pbcn (60) |
II Minimal non-isomorphic klassengleiche supergroups
- Additional centring translations
| [2] Ccc2 (37); [2] Amm2 (38); [2] Bbe2 (41, Aea2); [2] Ima2 (46) |
| [2] b' = 1/2b Pcc2 (27); [2] c' = 1/2c Pbm2 (28, Pma2) |