| Ten Calculations with tensors and characters M. Ephraim, T. Janssen, A. Janner and A. Thiers |
Next: Examples Up: The Buttons Previous: Tensor
- Point Group
- View Character Table
- Accept character table
- Power n=
- Add
- Product
- Power
- Symmetrized Square
- Antisymmetrized Square
- Physical character
- Decompose
- Copy
- Reset character list
- Close
Character
Starts the part of the program for calculations with characters of finite three-dimensional point groups.Point Group
Click on the button to open a menu for selecting a point group.View Character Table
Opens a separate window with the character table of the selected point group. Each column corresponds to a conjugation class.- Conjugation classes represented by elements expressed in terms of
generators
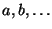 .
.
- The number of elements in each conjugation class.
- The order of the elements in the class.
- The characters of the irreducible representations.
- The classes to which the
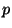 th power of an element of this
class belongs. These numbers are periodic with as period the order
of the elements of the class. The
th power of an element of this
class belongs. These numbers are periodic with as period the order
of the elements of the class. The 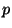 th power corresponds to the
th power corresponds to the
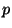 th row.
th row.
- The three-dimensional vector representation. Tensors can be obtained by taking (symmetrized or antisymmetrized) powers of the vector representation.
Accept character table
Presents in the character window the characters for the irreducible representations and the vector representation. They form the first lines in the list of characters.Power n=
The exponent needed for the specification of a power of a character.Add
Add two characters selected in the character window by clicking the buttons at the beginning of the line. The result is added as a new line in the character window.Product
Provides the product of two selected characters as a new line in the character list.Power
Provides theSymmetrized Square
Calculates the character of the representation which is the symmetrized second power of a selected representation by means of:Antisymmetrized Square
Calculates the character of the representation which is the antisymmetrized second power of a selected representation by means of:Physical character
For an irreducible representation it is checked whether it is also a physically irreducible representation. The expressionwhere
Decompose
Gives the multiplicities of the irreducible representations in the decomposition of the selected character.Copy
Copy the content of the character window to the worksheet, where it can be handled further.Reset character list
The selection buttons in front of the characters in the list in the character window are made inactive.Close
Close the character window and return to the worksheet.Next: Examples Up: The Buttons Previous: Tensor
