TenXar
 Calculations with tensors and characters

M. Ephraim, T. Janssen, A. Janner and A. Thiers

next up previous
Next: Character tables Up: Examples Previous: Examples

Subsections

Invariant tensors

Invariant magnetic field

A magnetic field transforms as a pseudotensor of rank one. For the point group m one has:

Dimension 3
Rank 1
Point group m (unique axis y)
Permutation symmetry 0
Basis transformation Identity
Type Pseudotensor

The result: One free parameter, T$_y =a$, T$_x$=T$_z$=0.

Metric tensor

A metric tensor is a symmetric tensor of rank two. In two dimensions one has for the point group 3:

Dimension 2
Rank 2
Point group 3
Permutation symmetry (0 1)
Basis transformation Identity
Type Tensor

The group is generated by a threefold rotation which is represented on a lattice basis by the matrix

\begin{displaymath}\begin{array}{rr} 0&-1 1&-1 \end{array} \end{displaymath}

The invariant tensor is:

\begin{displaymath}xx = yy =a,   xy = yx = -a .\end{displaymath}

This stands for the expression $a*(xx+yy-xy)$.

Metric tensor in three dimensions

The metric tensor invariant under the tetragonal group 4 follows from:

Dimension 3
Rank 2
Point group 4
Permutation symmetry (0 1)
Basis transformation Identity
Type Tensor

There are two free parameters:

\begin{displaymath} xx = yy = a,  zz = b,  xy=xz=yz=yx=zx=zy=0.\end{displaymath}

Elastic tensor

The elastic tensor is a rank-four tensor symmetric in the first two, the second two and exchange of first and second pair of indices.

Dimension 3
Rank 4
Point group 4
Permutation symmetry ((0 1)(2 3))
Basis transformation Identity
Type Tensor

Result:

\begin{displaymath} a*xxxx+b*xxxy+c*xxyy+d*xxzz+e*xyxy+f*xzxz+g*zzzz. \end{displaymath}

There are seven free parameters. For the standard notation where 1=$xx$, 2=$yy$, 3=$zz$, 4=$yz$, 5=$xz$, 6=$xy$ the elastic tensor becomes the 6$\times$6 matrix

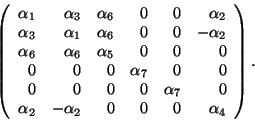
\begin{displaymath} \left( \begin{array}{rrrrrr} \alpha_1 & \alpha_3 &\alpha_6 &... ...7&0\\ \alpha_2&-\alpha_2&0&0&0&\alpha_4 \end{array} \right) . \end{displaymath}


\begin{displaymath} \alpha_1 = a, \alpha_2 =b/4, \alpha_3 =c/2, \alpha_4 =e/4, \alpha_5 =g,\alpha_6 =d/2,  \alpha_7 =f/4 . \end{displaymath}

Vector product

A vector product in three dimensions is an antisymmetric rank-two tensor. For the point group 4 one has:

Dimension 3
Rank 2
Point group 4
Permutation symmetry [0 1]
Basis transformation Identity
Type Pseudotensor

There is one free parameter:

$xy=-yx=a,     xx=xz=yy=yz=zx=zy=zz=0.$

Magnetoelectric tensor

An electric field $E$ may induce a magnetic field $M$: $M=\chi^{\rm ME}E$. It is a second-rank pseudotensor. For the point group mm2 one has

Dimension 3
Rank 2
Point group mm2 (unique axis z)
Permutation symmetry 0 1
Basis transformation Identity
Type Pseudotensor

There are two free parameters, and the elements of the invariant tensor are

$xy=a$, $yx=b$, $xx=yy=zz=xz=yz=zx=zy=0.$

next up previous
Next: Character tables Up: Examples Previous: Examples