| Ten Calculations with tensors and characters M. Ephraim, T. Janssen, A. Janner and A. Thiers |
Next: The Buttons Up: TenXar Previous: Introduction
QuickStart
The program is started by clicking on the icon in the window appearing after opening the CD-ROM. The program allows the determination of the general form of tensors and pseudotensors of arbitary rank, invariant under a chosen two- or three-dimensional crystallographic point group, and under given permutations of the indices. In the second part, calculations can be made with characters of arbitrary finite three- and two-dimensional point groups.The user is guided through the program with windows in which buttons can be clicked on to select pregiven choices, or with `fill-in' windows into which information can be typed. The functions of the various buttons are explained in the following section. We start with a guided tour. Clicking on the icon vol-d.exe opens a worksheet.
- Click on the button Tensor. An input window opens up.
- Type 3 in the open fill-in window behind Dimension.
- Type 2 in the open fill-in window Rank.
- Click on Point Group. A menu opens. Click on Orthorhombic. A new menu opens with the three point groups in the orthorhombic system. Click on 222. Now this point group is selected. You could also have typed 222 in the fill-in window of Point Group.
- The generators of the point group can be viewed in a separate window after having clicked on View Point Group. This can be closed by choosing Close under Window.
- Suppose we want to view the metric tensor for the point group 222,
which is a second-rank tensor
symmetric in both indices. Click on Perm. Symmetry and select (0 1).
The indices are denoted 0,..., through (rank
 1): here the rank is 2. Notice
that 0 1 is written without commas. To indicate that
the tensor is symmetric under permutation of both indices, 0 1 is put between
parentheses: select (0 1).
1): here the rank is 2. Notice
that 0 1 is written without commas. To indicate that
the tensor is symmetric under permutation of both indices, 0 1 is put between
parentheses: select (0 1).
- In the standard setting no basis transformation is needed: click Basis Transformation and then select No transformation.
- All information is now available. Click Tensor to determine the invariant tensor, which in our example is the metric tensor of a lattice in the orthorhombic system.
- After a period of time which depends on the dimension, the rank and the symmetry, the
results are presented in the main window, the worksheet. For convenience the
chosen point group and permutation symmetry are repeated, followed by the
number of free parameters in the invariant tensor.
The information about the tensor is a block with the following components:
- The dimension: 3.
- The rank: 2.
- The permutation symmetry: (0 1).
- The relations between the tensor elements, and the tensor elements expressed
in the free parameters.
The information given means: The three diagonal elements are nonzero and generally
different, all the off-diagonal elements are zero.
Thus in the window one finds:
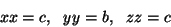
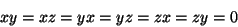
This means:
T
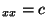 , T
, T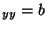 , T
, T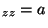
T
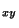 =T
=T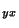 =0, T
=0, T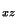 =T
=T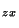 =0, T
=0, T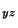 =T
=T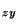 =0
=0
The invariant tensor then is written as
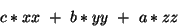
as a quadratic form, or as
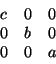
in matrix form.
The complete expression is
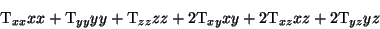
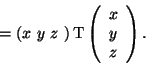
When there are too many free parameters (more than five) they are denoted as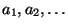 .
.
- The results can be shown in a separate window: click on To window at the left. The window that appears can be closed by the button in the left upper corner.
- The results can be kept in a file by clicking on To file and giving a file name, for example C:/temp/sample1.
- Repeat the sequence with the elasticity tensor. The dimension remains three. Click in the window behind Rank: 4.
- Select a point group. Click Point Group, click on Cubic, click on 432.
- Select the permutation symmetry, click on Perm. Symmetry, click on ((0 1)(2 3)).
- Select No basis transformation.
- Click on Tensor. The results appear on the worksheet, page 1. The tensor invariant under 432 and of type ((0 1)(2 3)) has three free parameters. The relations between the tensor elements are given, as well as their expression in terms of the free parameters.
- One can switch between the pages of the worksheet by means of the buttons Next and Previous.
- Close the input window by clicking Close.
- Click the button Character to use the second part. A new window (Character window) opens up.
- Select a point group, e.g. the point group 432.
- The character table for this point group can be viewed using View character
table. In a separate window this character table is presented as follows.
The first row gives representatives of the conjugation classes expressed in
generators. For 432 there are five classes (
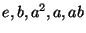 ). The second row gives
the number of elements in each of the (five) classes. The third row gives
the orders of the elements, e.g.
). The second row gives
the number of elements in each of the (five) classes. The third row gives
the orders of the elements, e.g. 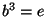 . Then follows a square matrix
with the characters arranged in columns for the classes and rows for the
irreducible representations. The next block contains the numbers of the
conjugation classes to which the
. Then follows a square matrix
with the characters arranged in columns for the classes and rows for the
irreducible representations. The next block contains the numbers of the
conjugation classes to which the 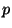 th power of an element of the class belongs.
In a column the numbers have as repetition rate the order of the elements in
the class. For example,
th power of an element of the class belongs.
In a column the numbers have as repetition rate the order of the elements in
the class. For example, 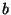 belongs to class 2,
belongs to class 2, 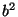 belongs to class 2 as well,
belongs to class 2 as well,
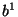 belongs to class 1,
belongs to class 1, 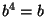 belongs to class 2 etc. The last row
gives the character of the three-dimensional vector representation, the representation
with which a vector transforms under the action of the chosen point group.
Close the window.
belongs to class 2 etc. The last row
gives the character of the three-dimensional vector representation, the representation
with which a vector transforms under the action of the chosen point group.
Close the window.
- Now click on Accept character table. This displays the characters of the irreducible representations and that of the vector representation in the character window.
- Operations on the characters can be performed. For a unary operation select one character in the character window, and click a button on the right-hand side (power, symmetric square, antisymmetric square). For a power the exponent is specified in the fill-in window n=. For a binary operation (add, product) select two characters by clicking the corresponding buttons at the left-hand side. These operations provide a new character that in the character window is added to the existing list. Clicking on Decompose yields the multiplicities of the irreducible characters in a selected character. Click on the button in front of irrep 3, fill in n=2 and click on Power. The square of the third character appears as the last line in the character window. Clicking the button in front and selecting Decompose yields the multiplicities (1 1 1 0 0) of the irreps on the worksheet. Selection of characters can be cancelled by clicking again, or clicking Reset character list.
- Selected characters in the character window can be transferred to the worksheet by means of Copy. There they can again be viewed using To window, or sent to a file using To file.
- The session can be closed by clicking Quit in the top line of the screen.
Next: The Buttons Up: TenXar Previous: Introduction
