[script p]62 6 Hexagonal
No. 55 [script p]62 Patterson symmetry [script p]6/m

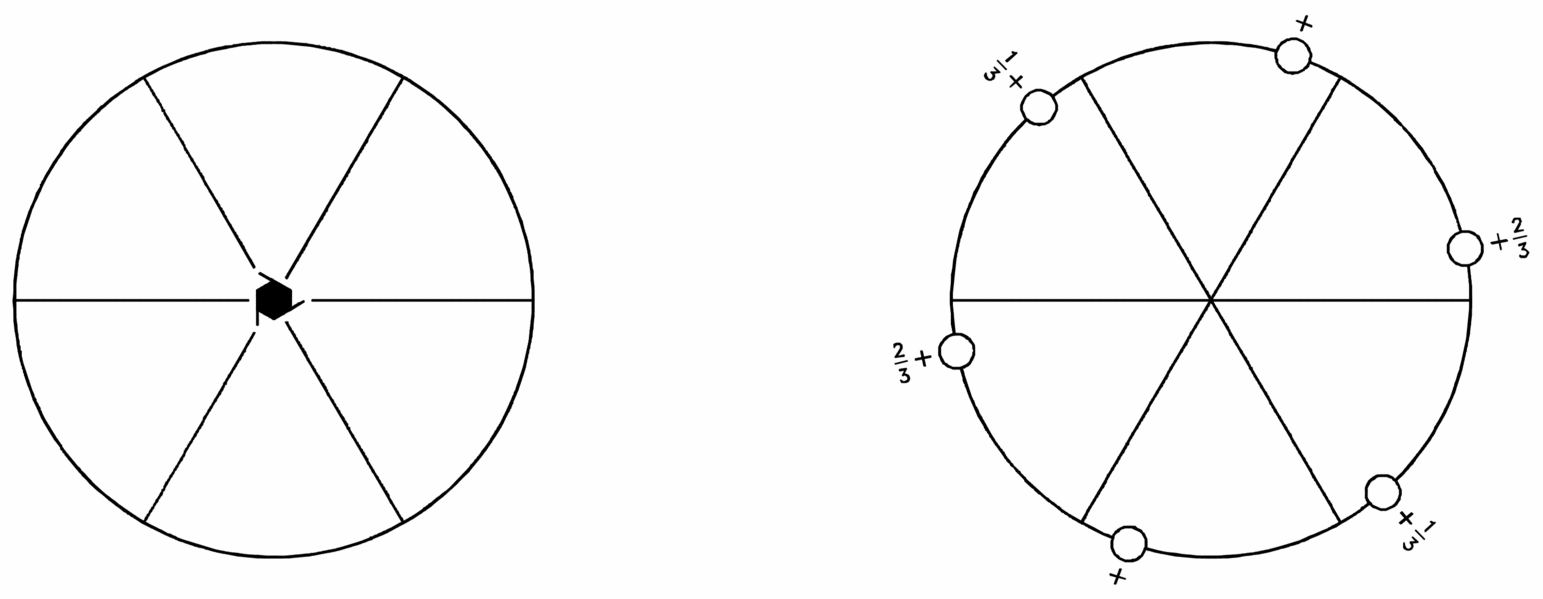
symmetry group diagram

Origin on 2 on 62

Asymmetric unit 0 ≤ x; 0 ≤ y; 0 ≤ z ≤ 1; y ≤ x

Symmetry operations

(1)  1   (2)  3+(2/3)   0, 0, z(3)  3-(1/3)   0, 0, z
(4)  2   0, 0, z(5)  6-(2/3)   0, 0, z(6)  6+(1/3)   0, 0, z

Generators selected (1); t(0, 0, 1); (2); (4)

Positions

Multiplicity, Wyckoff letter,
Site symmetry		 Coordinates Reflection conditions
 General:
6 b 1
(1) x, y, z(2) -y, x - y, z + 2/3(3) -x + y, -x, z + 1/3
(4) -x, -y, z(5) y, -x + y, z + 2/3(6) x - y, x, z + 1/3
l: l = 3n
  Special: no extra conditions
3 a  2 . . 
0, 0, z0, 0, z + 2/30, 0, z + 1/3

Symmetry of special projections

Along [001]   6

Origin at 0, 0, z 		Along [100]   [script p]11m
a' = c   
Origin at x, 0, 0 		Along [210]   [script p]11m
a' = c   
Origin at x, 1/2x, 0

Maximal non-isotypic non-enantiomorphic subgroups

I[2] [script p]32 (44)1; 2; 3
 [3] [script p]112 (8)1; 4
IIa none
IIb[2] [script p]61 (c' = 2c) (54)

Maximal isotypic subgroups and enantiomorphic subgroups of lowest index

IIc[2] [script p]64 (c' = 2c) (57); [7] [script p]62 (c' = 7c) (55)

Minimal non-isotypic non-enantiomorphic supergroups

I[2] [script p]6222 (64)
II[3] [script p]6 (c' = 1/3c) (53)








































to end of page
to top of page