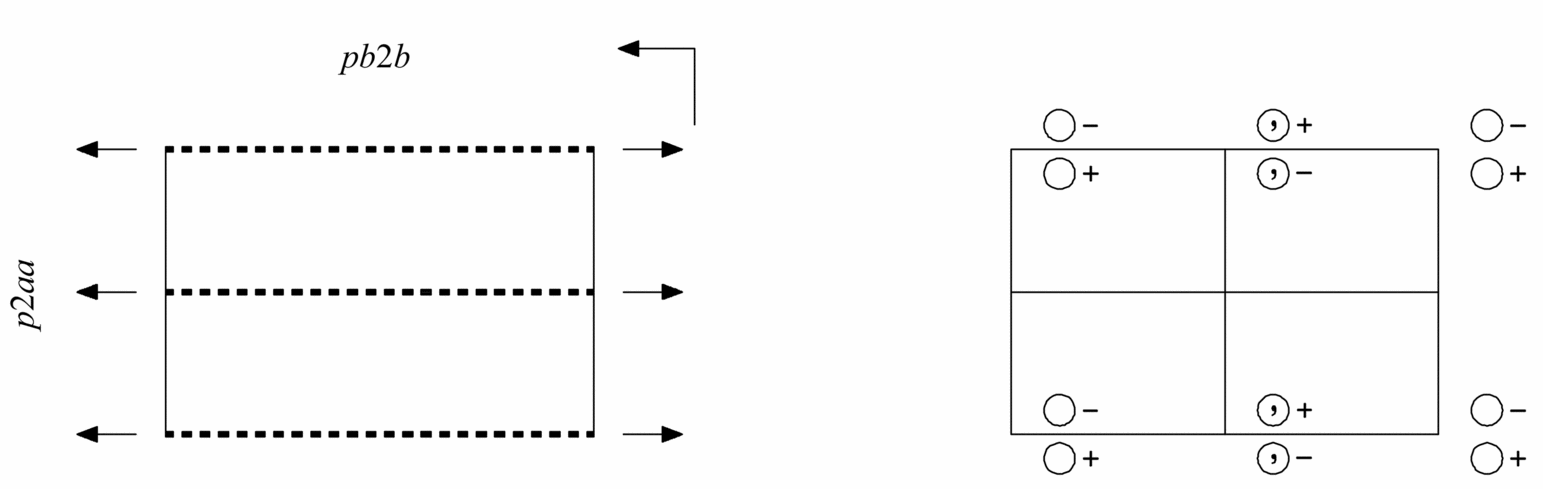
Origin on b2b

Asymmetric unit

0 ≤ x ≤ 1/2; 0 ≤ y ≤ 1; 0 ≤ z

(1)  1

(2)  2   0, y, 0

(3)  b   x, y, 0

(4)  b   0, y, z

Generators selected (1); t(1, 0, 0); t(0, 1, 0); (2); (3)

Positions

Multiplicity, Wyckoff letter, Site symmetry	Coordinates	Reflection conditions
		General:
4 c 1	(1) x, y, z (2) -x, y, -z (3) x, y + 1/2, -z (4) -x, y + 1/2, z	hk: k = 2n 0k: k = 2n

		Special: no extra conditions
2 b  . 2 .	1/2, y, 0 1/2, y + 1/2, 0
2 a  . 2 .	0, y, 0 0, y + 1/2, 0

Symmetry of special projections

Along [001]   p1m1 a' = a   b' = 1/2b    Origin at 0, 0, z

Along [100]   11m a' = 1/2b    Origin at x, 0, 0

Along [010]   2mm a' = a    Origin at 0, y, 0

Maximal non-isotypic subgroups

---

I	[2] pb11 (12)	1; 4
	[2] p121 (p211, 8)	1; 2
	[2] p11b (p11a, 5)	1; 3

IIa

none

IIb	[2] pb2n (a' = 2a) (34)

Maximal isotypic subgroups of lowest index

---

IIc	[2] pb2b (a' = 2a) (30); [3] pb2b (b' = 3b) (30)

Minimal non-isotypic supergroups

---

I	[2] pmaa (38); [2] pbaa (43)

II	[2] cm2e (36); [2] pm2m (b' = 1/2b) (27)

---