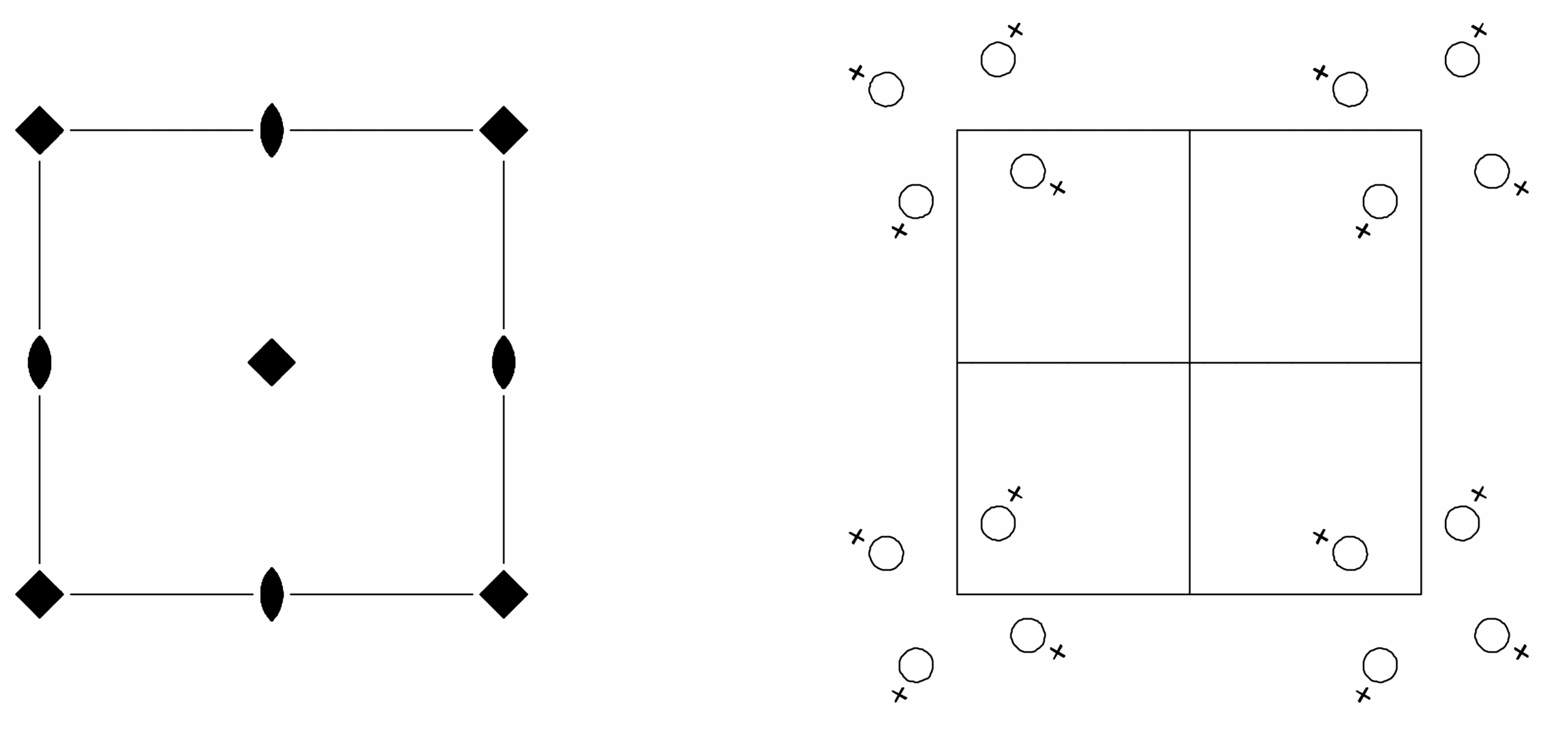
Origin on 4

Asymmetric unit

0 ≤ x ≤ 1/2; 0 ≤ y ≤ 1/2

(1)  1

(2)  2   0, 0, z

(3)  4+   0, 0, z

(4)  4-   0, 0, z

Generators selected (1); t(1, 0, 0); t(0, 1, 0); (2); (3)

Positions

Multiplicity, Wyckoff letter, Site symmetry	Coordinates	Reflection conditions
		General:
4 d 1	(1) x, y, z (2) -x, -y, z (3) -y, x, z (4) y, -x, z	no conditions

		Special:
2 c  2 . .	0, 1/2, z 1/2, 0, z	hk: h + k = 2n
1 b  4 . .	1/2, 1/2, z	no extra conditions
1 a  4 . .	0, 0, z	no extra conditions

Symmetry of special projections

Along [001]   p4 a' = a   b' = b    Origin at 0, 0, z

Along [100]   1m1 a' = b    Origin at x, 0, 0

Along [110]   1m1 a' = 1/2(-a + b)    Origin at x, x, 0

Maximal non-isotypic subgroups

---

I

[2] p211 (p112, 3)

1; 2

IIa

none

IIb

none

Maximal isotypic subgroups of lowest index

---

IIc	[2] c4 (a' = 2a, b' = 2b) (p4, 49)

Minimal non-isotypic supergroups

---

I	[2] p4/m (51); [2] p4/n (52); [2] p422 (53); [2] p4212 (54); [2] p4mm (55); [2] p4bm (56)

II

none

---