International Tables for Crystallography
Symmetry database
doi: 10.1107/97809553602060000112
 | This database is a unique resource that provides more extensive symmetry information than can be found in the print editions of International Tables for Crystallography Volumes A and A1. This additional symmetry information can either be retrieved directly from the database or simple calculations can be carried out using the database to generate specific data 'on the fly'. Use of the symmetry database thus facilitates the in-depth study of group-subgroup relations, domain structures and twinning, families of related crystal structures and phase transitions, and the prediction of new crystal structures. 3D interactive visualization of space-group and point-group symmetries is also provided. A comprehensive guide to the many different features and uses of the symmetry database is given in the article by de la Flor et al. [J. Appl. Cryst. (2023). 56, 1824-1840]. | access the symmetry database | help | |
About the symmetry database
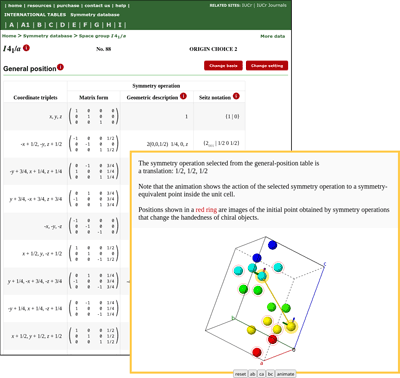
In the symmetry database, the data in Volume A are extended to include the generators, general positions and Wyckoff positions of all 230 space groups, including the 530 settings for the monoclinic and orthorhombic space groups listed in Table 1.5.4.4 of Volume A. If data are not available for a particular setting directly, an arbitrary basis transformation can be specified and the data will be transformed to this new basis. 3D interactive visualization of the general-position diagrams using JMol, including animation of the actions of screw rotations and glide reflections, allows users to explore space-group symmetry for themselves.
The maximal subgroup data given in Volume A1 are extended in the symmetry database to subgroups of arbitrary index for all the space groups, and series of isomorphic subgroups are available in a parametric form for indices up to 50 for orthorhombic, tetragonal, trigonal and hexagonal space groups and for indices up to 27 and 125 for cubic space groups. Interactive contracted and complete graphs of chains of maximal subgroups, including basis transformations and origin shifts for each step, can also be generated, and an easy-to-follow step-by-step procedure is provided to allow the user to determine the transformation matrix between the group and subgroup if this is not already known. In addition, data for supergroups of arbitrary index of all the space groups are provided. In contrast to Volume A1, where only space-group types of supergroups are indicated, in the symmetry database each supergroup is listed individually and specified by the transformation matrix that relates the conventional bases of the group and the supergroup. The subgroup and supergroup data can be transformed to the basis of the group. Left and right coset decomposition calculations can be carried out, and Wyckoff-position splittings can be obtained along with the relations between the coordinates of the positions within the group and subgroup.
Information is also available for the Euclidean, chirality-preserving and affine normalizers of the space groups; these aid many crystallographic calculations including the comparison of different coordinate descriptions of a crystal structure (and the accompanying changes in structure factors) and the derivation of phase restrictions for use in direct methods, as described in Chapter 3.5 of Volume A.
For those interested in molecular symmetry and the physical properties of materials, the generators, general and special positions, and Wyckoff positions of the 3D crystallographic point groups are presented and can be transformed to different settings, enhancing and extending the data presented in Chapter 3.2 of Volume A. Simple, clear and instructive interactive visualization of the symmetry elements of the crystallographic point groups is provided.
Throughout the database, symmetry operations are presented in four different ways to suit a range of purposes: as x, y, z-based coordinate triplets, in matrix form, by geometric symbols (indicating the type and order of the operations, and the orientation of the corresponding symmetry elements) and in Seitz notation.
Site-symmetry groups, showing how the symmetry elements at a site are related to the symmetry elements of the crystal lattice, are also listed for the space and point groups.
Help can be obtained throughout the database by clicking on the help symbols  provided.
provided.