|
Axes |
Coordinates |
Wyckoff positions |
|
|
|
4a |
4b |
4c |
4d |
8e |
| I Maximal translationengleiche subgroups |
| [2] Pnn2 (34) |
|
x + (1/4), y, z |
4c |
4c |
2a; 2b |
4c |
2 × 4c |
| [2] Pn21a (33) |
|
x + (1/4), y, z + (1/4) |
4a |
4a |
4a |
4a |
2 × 4a |
![[conventional setting]](/graphics/sg/Wconv.gif) Pna21 Pna21 |
a, c, -b |
x + (1/4), z + (1/4), -y |
|
|
|
|
|
| [2] P2na (30) |
|
x, y + (1/4), z + (1/4) |
4c |
4c |
4c |
2a; 2b |
2 × 4c |
![[conventional setting]](/graphics/sg/Wconv.gif) Pnc2 Pnc2 |
b, c, a |
y + (1/4), z + (1/4), x |
|
|
|
|
|
| [2] P2212 (17) |
|
x + (1/4), y, z + (1/4) |
4e |
4e |
2a; 2b |
2c; 2d |
2 × 4e |
![[conventional setting]](/graphics/sg/Wconv.gif) P2221 P2221 |
c, a, b |
z + (1/4), x + (1/4), y |
|
|
|
|
|
| [2] P121/n1 (14) |
|
|
2a; 2d |
2b; 2c |
4e |
4e |
2 × 4e |
| [2] P2/n11 (13) |
|
|
2a; 2c |
2b; 2d |
4g |
2e; 2f |
2 × 4g |
![[conventional setting]](/graphics/sg/Wconv.gif) P12/n1 P12/n1 |
c, a, b |
z, x, y |
|
|
|
|
|
| [2] P112/a (13) |
|
|
2a; 2b |
2c; 2d |
2e; 2f |
4g |
2 × 4g |
![[conventional setting]](/graphics/sg/Wconv.gif) P12/c1 P12/c1 |
b, c, a |
y, z, x |
|
|
|
|
|
| II Maximal klassengleiche subgroups |
| Enlarged unit cell, isomorphic |
| [3] Pnna |
3a, b, c |
(1/3)x, y, z; ±((1/3), 0, 0) |
4a; 8e |
4b; 8e |
4c; 8e |
3 × 4d |
3 × 8e |
| [p] Pnna |
pa, b, c |
(1/p)x, y, z; +((u/p), 0, 0) |
4a; ((p - 1)/2) × 8e |
4b; ((p - 1)/2) × 8e |
4c; ((p - 1)/2) × 8e |
p × 4d |
p × 8e |
|
p = prime > 2; u = 1, . . ., p - 1 |
|
|
|
|
|
| [3] Pnna |
a, 3b, c |
x, (1/3)y, z; ±(0, (1/3), 0) |
4a; 8e |
4b; 8e |
4c; 8e |
4d; 8e |
3 × 8e |
| [p] Pnna |
a, pb, c |
x, (1/p)y, z; +(0, (u/p), 0) |
4a; ((p - 1)/2) × 8e |
4b; ((p - 1)/2) × 8e |
4c; ((p - 1)/2) × 8e |
4d; ((p - 1)/2) × 8e |
p × 8e |
|
p = prime > 2; u = 1, . . ., p - 1 |
|
|
|
|
|
| [3] Pnna |
a, b, 3c |
x, y, (1/3)z; ±(0, 0, (1/3)) |
4a; 8e |
4b; 8e |
3 × 4c |
4d; 8e |
3 × 8e |
| [p] Pnna |
a, b, pc |
x, y, (1/p)z; +(0, 0, (u/p)) |
4a; ((p - 1)/2) × 8e |
4b; ((p - 1)/2) × 8e |
p × 4c |
4d; ((p - 1)/2) × 8e |
p × 8e |
|
p = prime > 2; u = 1, . . ., p - 1 |
|
|
|
|
|
![[conventional setting]](/graphics/sg/Wconv.gif) Pna21
Pna21![[conventional setting]](/graphics/sg/Wconv.gif) Pnc2
Pnc2![[conventional setting]](/graphics/sg/Wconv.gif) P2221
P2221![[conventional setting]](/graphics/sg/Wconv.gif) P12/n1
P12/n1![[conventional setting]](/graphics/sg/Wconv.gif) P12/c1
P12/c1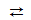 b
b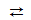 -b
-b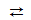 -y
-y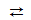 c
c -c
-c -z
-z c
c -c
-c -z
-z
