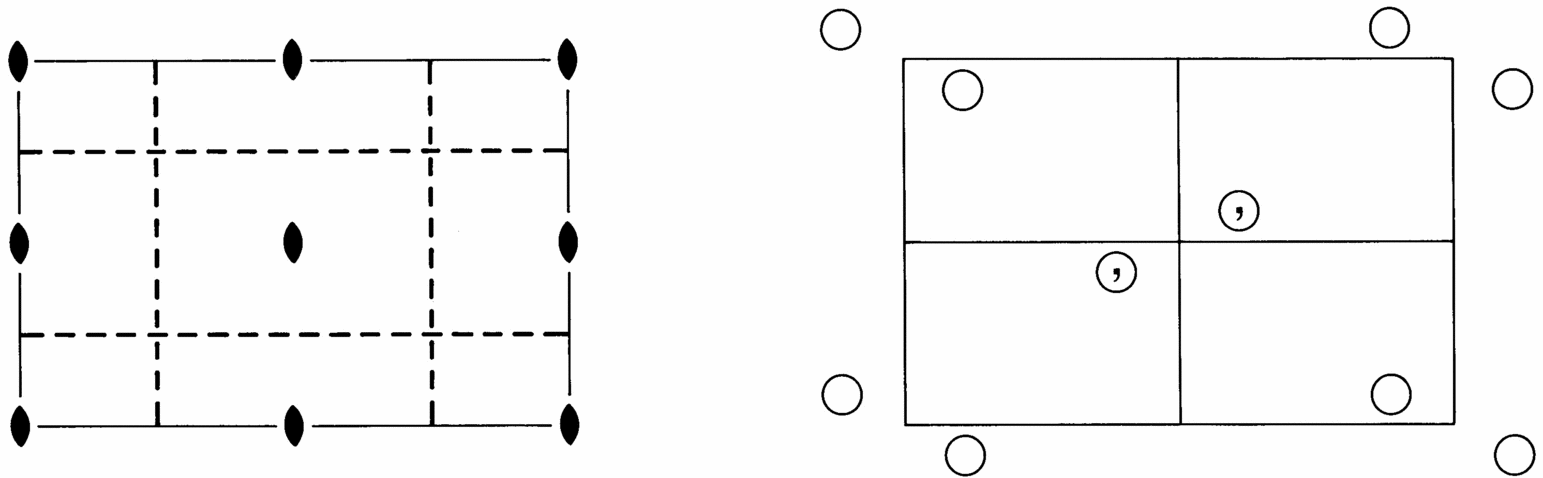
Move your mouse over or click on the links to get information about each item. Detailed information on the space-group tables is given in Chapter 2.2.

Origin at 2

Asymmetric unit

0 ≤ x ≤ 1/2; 0 ≤ y ≤ 1/2

(1)  1

(2)  2   0, 0

(3)  b   1/4, y

(4)  a   x, 1/4

Generators selected (1); t(1, 0); t(0, 1); (2); (3)

Positions

Multiplicity, Wyckoff letter, Site symmetry	Coordinates	Reflection conditions
		General:
4 c 1	(1) x, y (2) -x, -y (3) -x + 1/2, y + 1/2 (4) x + 1/2, -y + 1/2	h0 : h = 2n 0k : k = 2n

		Special: as above, plus
2 b  2 . .	1/2, 0 0, 1/2	hk : h + k = 2n
2 a  2 . .	0, 0 1/2, 1/2	hk : h + k = 2n

Maximal non-isomorphic subgroups

---

I	[2] p1g1 (pg, 4)	1; 3
	[2] p11g (pg, 4)	1; 4
	[2] p211 (p2, 2)	1; 2

IIa

none

IIb

none

Maximal isomorphic subgroups of lowest index

---

IIc	[3] p2gg  (a' = 3a or b' = 3b) (8)

Minimal non-isomorphic supergroups

---

I	[2] p4gm (12)

II	[2] c2mm (9); [2] p2mg (a' = 1/2 a) (7); [2] p2gm (b' = 1/2 b) (p2mg, 7)

---