P2/m C2h1 2/m Monoclinic info
No. 10 P12/m1 Patterson symmetry P12/m1
UNIQUE AXIS b

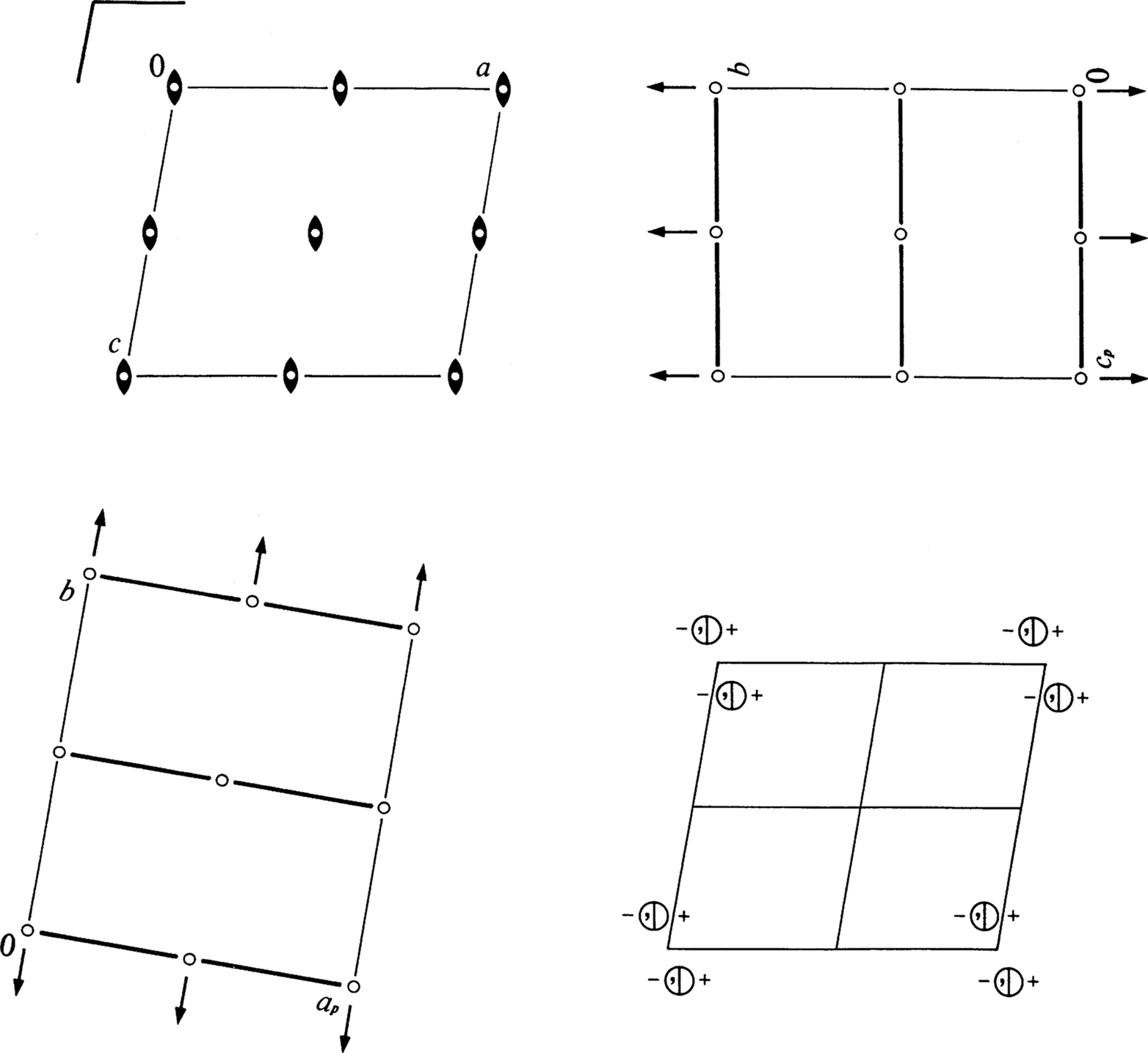
symmetry group diagram

Origin at centre (2/m)

Asymmetric unit 0 ≤ x ≤ 1/2; 0 ≤ y ≤ 1/2; 0 ≤ z ≤ 1

Symmetry operations

(1)  1   (2)  2   0, y, 0(3)  -1   0, 0, 0(4)  m   x, 0, z

Generators selected (1); t(1, 0, 0); t(0, 1, 0); t(0, 0, 1); (2); (3)

Positions

Multiplicity, Wyckoff letter,
Site symmetry		 Coordinates Reflection conditions
 General:
4 o 1
(1) x, y, z(2) -x, y, -z(3) -x, -y, -z(4) x, -y, z
no conditions
    Special: as above, plus
2 n  m 
x, 1/2, z -x, 1/2, -z
no extra conditions
2 m  m 
x, 0, z -x, 0, -z
no extra conditions
2 l  2 
1/2, y, 1/2 1/2, -y, 1/2
no extra conditions
2 k  2 
0, y, 1/2 0, -y, 1/2
no extra conditions
2 j  2 
1/2, y, 0 1/2, -y, 0
no extra conditions
2 i  2 
0, y, 0 0, -y, 0
no extra conditions
1 h  2/m 
1/2, 1/2, 1/2
no extra conditions
1 g  2/m 
1/2, 0, 1/2
no extra conditions
1 f  2/m 
0, 1/2, 1/2
no extra conditions
1 e  2/m 
1/2, 1/2, 0
no extra conditions
1 d  2/m 
1/2, 0, 0
no extra conditions
1 c  2/m 
0, 0, 1/2
no extra conditions
1 b  2/m 
0, 1/2, 0
no extra conditions
1 a  2/m 
0, 0, 0
no extra conditions

Symmetry of special projections

Along [001]   p2mm
a' = ap   b' = b   
Origin at 0, 0, z		Along [100]   p2mm
a' = b   b' = cp   
Origin at x, 0, 0		Along [010]   p2
a' = c   b' = a   
Origin at 0, y, 0

Maximal non-isomorphic subgroups

I [2] P1m1 (Pm, 6)1; 4
  [2] P121 (P2, 3)1; 2
  [2] P-1 (2)1; 3
IIa none
IIb[2] P121/m1 (b' = 2b) (P21/m, 11); [2] P12/c1 (c' = 2c) (P2/c, 13); [2] P12/a1 (a' = 2a) (P2/c, 13); [2] B12/e1 (a' = 2a, c' = 2c) (P2/c, 13); [2] C12/m1 (a' = 2a, b' = 2b) (C2/m, 12); [2] A12/m1 (b' = 2b, c' = 2c) (C2/m, 12); [2] F12/m1 (a' = 2a, b' = 2b, c' = 2c) (C2/m, 12)

Maximal isomorphic subgroups of lowest index

IIc[2] P12/m1 (b' = 2b) (P2/m, 10); [2] P12/m1 (c' = 2c or a' = 2a or a' = a + c, c' = -a + c) (P2/m, 10)

Minimal non-isomorphic supergroups

I[2] Pmmm (47); [2] Pccm (49); [2] Pmma (51); [2] Pmna (53); [2] Pbam (55); [2] Pnnm (58); [2] Cmmm (65); [2] Cccm (66); [2] P4/m (83); [2] P42/m (84); [3] P6/m (175)
II[2] C12/m1 (C2/m, 12); [2] A12/m1 (C2/m, 12); [2] I12/m1 (C2/m, 12)








































to end of page
to top of page