| Ccc2 | C2v13 | mm2 | Orthorhombic  |
| No. 37 | Ccc2 | Patterson symmetry Cmmm | |
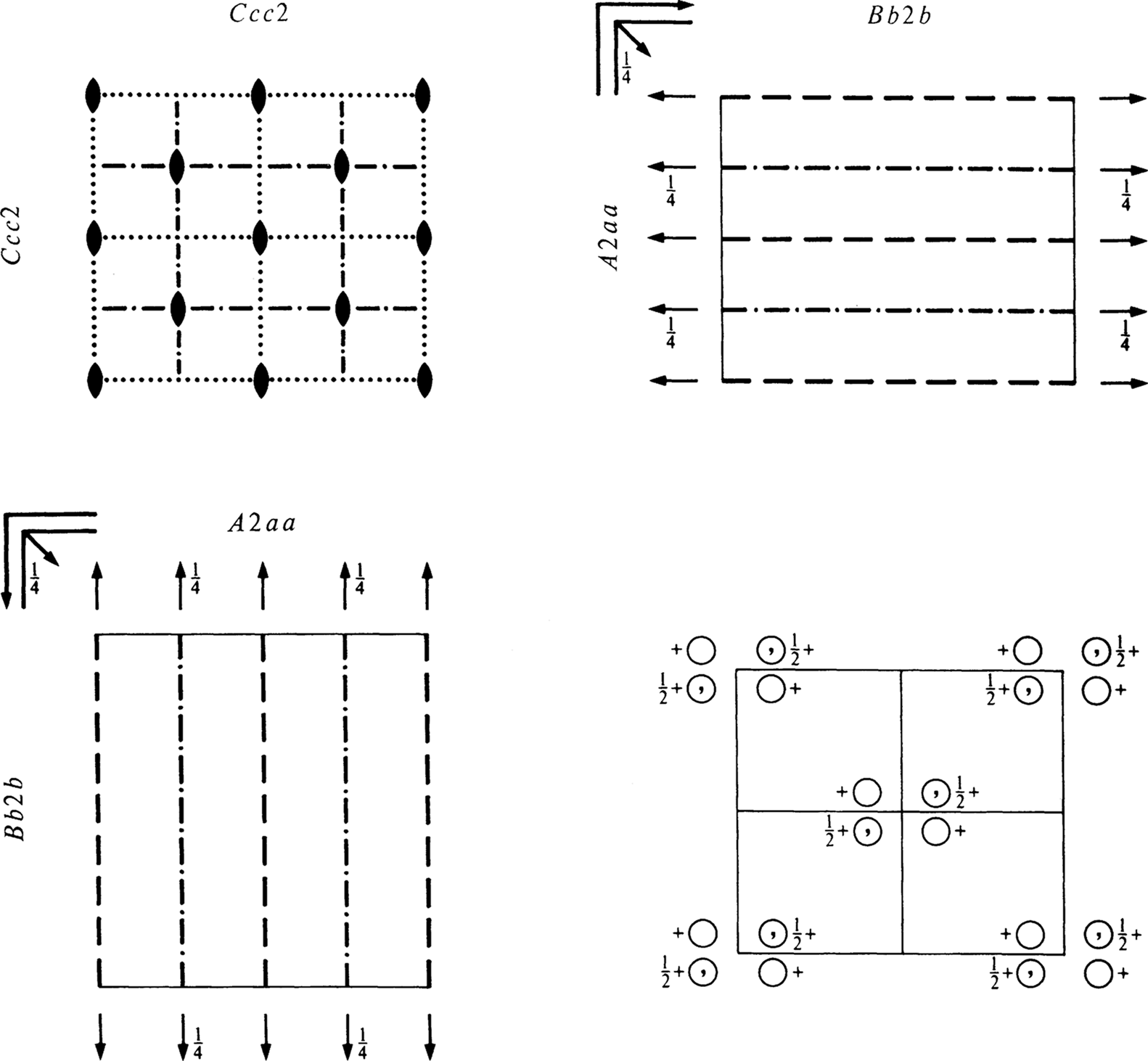
Origin on c c 2
| Asymmetric unit | 0 ≤ x ≤ 1/4; 0 ≤ y ≤ 1/2; 0 ≤ z ≤ 1 |
Symmetry operations
For (0, 0, 0)+ set
| (1) 1 | (2) 2 0, 0, z | (3) c x, 0, z | (4) c 0, y, z |
For (1/2, 1/2, 0)+ set
| (1) t(1/2, 1/2, 0) | (2) 2 1/4, 1/4, z | (3) n(1/2, 0, 1/2) x, 1/4, z | (4) n(0, 1/2, 1/2) 1/4, y, z |
Generators selected (1); t(1, 0, 0); t(0, 1, 0); t(0, 0, 1); t(1/2, 1/2, 0); (2); (3)
Positions
| Multiplicity, Wyckoff letter, Site symmetry | Coordinates | Reflection conditions | |||||||
| (0, 0, 0)+ (1/2, 1/2, 0)+ | General: | ||||||||
|
| hkl : h + k = 2n 0kl : k, l = 2n h0l : h, l = 2n hk0 : h + k = 2n h00 : h = 2n 0k0 : k = 2n 00l : l = 2n |
| Special: as above, plus | |||||||
|
| hkl : k + l = 2n | |||||
|
| hkl : l = 2n | |||||
|
| hkl : l = 2n |
Symmetry of special projections
| Along [001] c2mm a' = a b' = b Origin at 0, 0, z | Along [100] p1m1 a' = 1/2b b' = 1/2c Origin at x, 0, 0 | Along [010] p11m a' = 1/2c b' = 1/2a Origin at 0, y, 0 |
Maximal non-isomorphic subgroups
| I | [2] C1c1 (Cc, 9) | (1; 3)+ | |
| [2] Cc11 (Cc, 9) | (1; 4)+ | ||
| [2] C112 (P2, 3) | (1; 2)+ |
| IIa | [2] Pnn2 (34) | 1; 2; (3; 4) + (1/2, 1/2, 0) | |
| [2] Pnc2 (30) | 1; 3; (2; 4) + (1/2, 1/2, 0) | ||
| [2] Pcn2 (Pnc2, 30) | 1; 4; (2; 3) + (1/2, 1/2, 0) | ||
| [2] Pcc2 (27) | 1; 2; 3; 4 |
| IIb | none |
Maximal isomorphic subgroups of lowest index
| IIc | [3] Ccc2 (a' = 3a or b' = 3b) (37); [3] Ccc2 (c' = 3c) (37) |
Minimal non-isomorphic supergroups
| I | [2] Cccm (66); [2] Ccce (68); [2] P4cc (103); [2] P4nc (104); [2] P42mc (105); [2] P42bc (106); [2] P-42c (112); [2] P-421c (114); [3] P6cc (184) |
| II | [2] Fmm2 (42); [2] Pcc2 (a' = 1/2a, b' = 1/2b) (27); [2] Cmm2 (c' = 1/2c) (35) |
