P32 C33 3 Trigonal info
No. 145 P32 Patterson symmetry P-3

symmetry group diagram

Origin on 32

Asymmetric unit 0 ≤ x ≤ 1; 0 ≤ y ≤ 1; 0 ≤ z ≤ 1/3
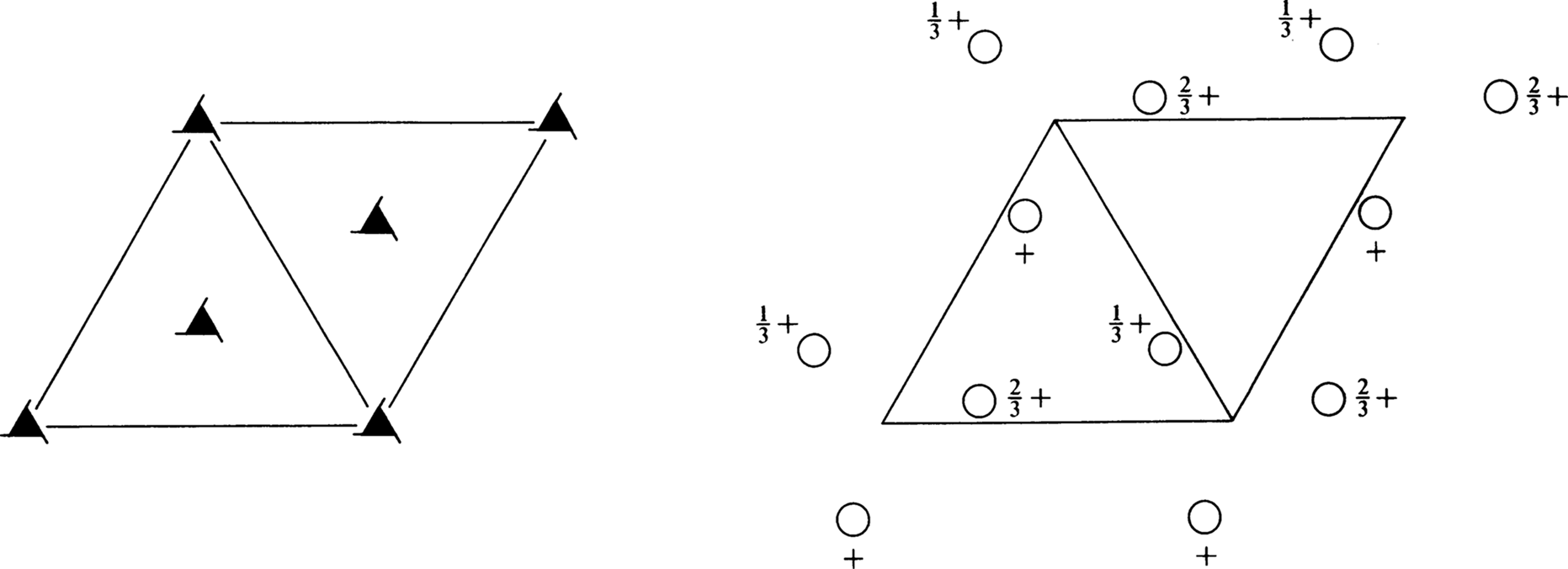
Vertices
0, 0, 0  1, 0, 0  1, 1, 0  0, 1, 0  
0, 0, 1/3  1, 0, 1/3  1, 1, 1/3  0, 1, 1/3  

Symmetry operations

(1)  1   (2)  3+(0, 0, 2/3)   0, 0, z(3)  3-(0, 0, 1/3)   0, 0, z

Generators selected (1); t(1, 0, 0); t(0, 1, 0); t(0, 0, 1); (2)

Positions

Multiplicity, Wyckoff letter,
Site symmetry		 Coordinates Reflection conditions
 General:
3 a 1
(1) x, y, z(2) -y, x - y, z + 2/3(3) -x + y, -x, z + 1/3
000l : l = 3n

Symmetry of special projections

Along [001]   p3
a' = a   b' = b   
Origin at 0, 0, z		Along [100]   p1
a' = 1/2(a + 2b)   b' = c   
Origin at x, 0, 0		Along [210]   p1
a' = 1/2b   b' = c   
Origin at x, 1/2x, 0

Maximal non-isomorphic subgroups

I [3] P1 (1)1
IIa none
IIbnone

Maximal isomorphic subgroups of lowest index

IIc[2] P31 (c' = 2c) (144); [3] H32 (a' = 3a, b' = 3b) (P32, 145); [7] P32 (c' = 7c) (145)

Minimal non-isomorphic supergroups

I[2] P3212 (153); [2] P3221 (154); [2] P65 (170); [2] P62 (171)
II[3] R3 (obverse) (146); [3] R3 (reverse) (146); [3] P3 (c' = 1/3c) (143)








































to end of page
to top of page