Pnnn D2h2 mmm Orthorhombic info
No. 48 P2/n2/n2/n Patterson symmetry Pmmm
ORIGIN CHOICE 2

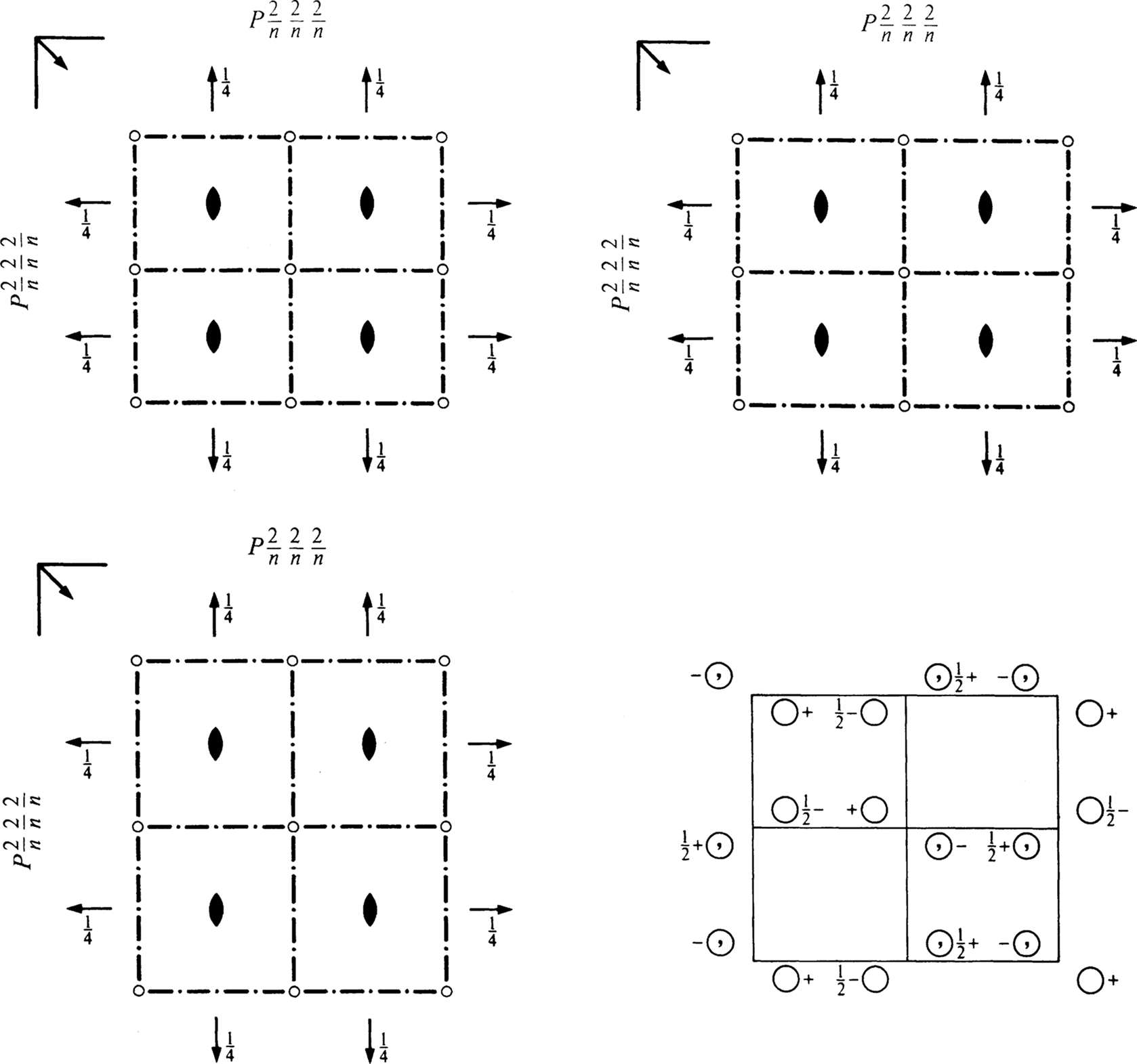
symmetry group diagram

Origin at -1 at n n n, at -1/4, -1/4, -1/4 from 2 2 2

Asymmetric unit 0 ≤ x ≤ 1/4; -1/4 ≤ y ≤ 1/4; 0 ≤ z ≤ 1

Symmetry operations

(1)  1   (2)  2   1/4, 1/4, z(3)  2   1/4, y, 1/4(4)  2   x, 1/4, 1/4
(5)  -1   0, 0, 0(6)  n(1/2, 1/2, 0)   x, y, 0(7)  n(1/2, 0, 1/2)   x, 0, z(8)  n(0, 1/2, 1/2)   0, y, z

Generators selected (1); t(1, 0, 0); t(0, 1, 0); t(0, 0, 1); (2); (3); (5)

Positions

Multiplicity, Wyckoff letter,
Site symmetry		 Coordinates Reflection conditions
 General:
8 m 1
(1) x, y, z(2) -x + 1/2, -y + 1/2, z(3) -x + 1/2, y, -z + 1/2(4) x, -y + 1/2, -z + 1/2
(5) -x, -y, -z(6) x + 1/2, y + 1/2, -z(7) x + 1/2, -y, z + 1/2(8) -x, y + 1/2, z + 1/2
0kl : k + l = 2n
h0l : h + l = 2n
hk0 : h + k = 2n
h00 : h = 2n
0k0 : k = 2n
00l : l = 2n
    Special: as above, plus
4 l  . . 2 
1/4, 3/4, z 1/4, 3/4, -z + 1/2 3/4, 1/4, -z 3/4, 1/4, z + 1/2
hkl : h + k + l = 2n
4 k  . . 2 
1/4, 1/4, z 1/4, 1/4, -z + 1/2 3/4, 3/4, -z 3/4, 3/4, z + 1/2
hkl : h + k + l = 2n
4 j  . 2 . 
3/4, y, 1/4 3/4, -y + 1/2, 1/4 1/4, -y, 3/4 1/4, y + 1/2, 3/4
hkl : h + k + l = 2n
4 i  . 2 . 
1/4, y, 1/4 1/4, -y + 1/2, 1/4 3/4, -y, 3/4 3/4, y + 1/2, 3/4
hkl : h + k + l = 2n
4 h  2 . . 
x, 1/4, 3/4 -x + 1/2, 1/4, 3/4 -x, 3/4, 1/4x + 1/2, 3/4, 1/4
hkl : h + k + l = 2n
4 g  2 . . 
x, 1/4, 1/4 -x + 1/2, 1/4, 1/4 -x, 3/4, 3/4x + 1/2, 3/4, 3/4
hkl : h + k + l = 2n
4 f  -1 
0, 0, 0 1/2, 1/2, 0 1/2, 0, 1/2 0, 1/2, 1/2
hkl : h + k, h + l, k + l = 2n
4 e  -1 
1/2, 1/2, 1/2 0, 0, 1/2 0, 1/2, 0 1/2, 0, 0
hkl : h + k, h + l, k + l = 2n
2 d  2 2 2 
1/4, 3/4, 1/4 3/4, 1/4, 3/4
hkl : h + k + l = 2n
2 c  2 2 2 
1/4, 1/4, 3/4 3/4, 3/4, 1/4
hkl : h + k + l = 2n
2 b  2 2 2 
3/4, 1/4, 1/4 1/4, 3/4, 3/4
hkl : h + k + l = 2n
2 a  2 2 2 
1/4, 1/4, 1/4 3/4, 3/4, 3/4
hkl : h + k + l = 2n

Symmetry of special projections

Along [001]   c2mm
a' = a   b' = b   
Origin at 1/4, 1/4, z		Along [100]   c2mm
a' = b   b' = c   
Origin at x, 1/4, 1/4		Along [010]   c2mm
a' = c   b' = a   
Origin at 1/4, y, 1/4

Maximal non-isomorphic subgroups

I [2] Pnn2 (34)1; 2; 7; 8
  [2] Pn2n (Pnn2, 34)1; 3; 6; 8
  [2] P2nn (Pnn2, 34)1; 4; 6; 7
  [2] P222 (16)1; 2; 3; 4
  [2] P112/n (P2/c, 13)1; 2; 5; 6
  [2] P12/n1 (P2/c, 13)1; 3; 5; 7
  [2] P2/n11 (P2/c, 13)1; 4; 5; 8
IIa none
IIb[2] Fddd (a' = 2a, b' = 2b, c' = 2c) (70)

Maximal isomorphic subgroups of lowest index

IIc[3] Pnnn (a' = 3a or b' = 3b or c' = 3c) (48)

Minimal non-isomorphic supergroups

I[2] P4/nnc (126); [2] P42/nnm (134); [3] Pn-3 (201)
II[2] Immm (71); [2] Amaa (Cccm, 66); [2] Bbmb (Cccm, 66); [2] Cccm (66); [2] Pncb (a' = 1/2a) (Pban, 50); [2] Pcna (b' = 1/2b) (Pban, 50); [2] Pban (c' = 1/2c) (50)








































to end of page
to top of page