P31c C3v4 31m Trigonal info
No. 159 P31c Patterson symmetry P-31m

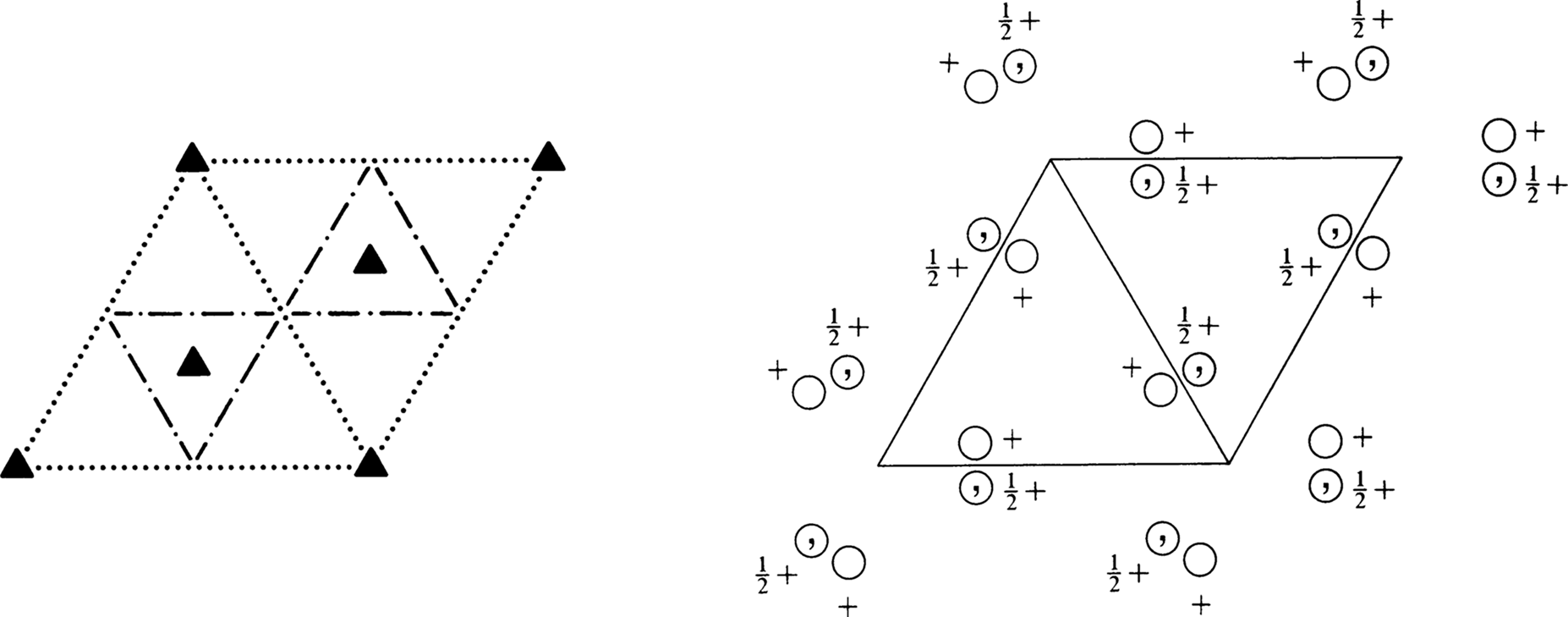
symmetry group diagram

Origin on 3 1 c

Asymmetric unit 0 ≤ x ≤ 2/3; 0 ≤ y ≤ 2/3; 0 ≤ z ≤ 1/2; x ≤ (1 + y)/2; y ≤ min(1 - x, (1 + x)/2)
Vertices
0, 0, 0  1/2, 0, 0  2/3, 1/3, 0  1/3, 2/3, 0  0, 1/2, 0  
0, 0, 1/2  1/2, 0, 1/2  2/3, 1/3, 1/2  1/3, 2/3, 1/2  0, 1/2, 1/2  

Symmetry operations

(1)  1   (2)  3+   0, 0, z(3)  3-   0, 0, z
(4)  c   x, x, z(5)  c   x, 0, z(6)  c   0, y, z

Generators selected (1); t(1, 0, 0); t(0, 1, 0); t(0, 0, 1); (2); (4)

Positions

Multiplicity, Wyckoff letter,
Site symmetry		 Coordinates Reflection conditions
 General:
6 c 1
(1) x, y, z(2) -y, x - y, z(3) -x + y, -x, z
(4) y, x, z + 1/2(5) x - y, -y, z + 1/2(6) -x, -x + y, z + 1/2
hh(-2h)l : l = 2n
000l : l = 2n
    Special: as above, plus
2 b  3 . . 
1/3, 2/3, z 2/3, 1/3, z + 1/2
hkil : l = 2n
or h - k = 3n + 1
or h - k = 3n + 2
2 a  3 . . 
0, 0, z 0, 0, z + 1/2
hkil : l = 2n

Symmetry of special projections

Along [001]   p31m
a' = a   b' = b   
Origin at 0, 0, z		Along [100]   p1g1
a' = 1/2(a + 2b)   b' = c   
Origin at x, 0, 0		Along [210]   p1
a' = 1/2b   b' = 1/2c   
Origin at x, 1/2x, 0

Maximal non-isomorphic subgroups

I [2] P311 (P3, 143)1; 2; 3
 [brace][3] P11c (Cc, 9)1; 4
 [3] P11c (Cc, 9)1; 5
 [3] P11c (Cc, 9)1; 6
IIa none
IIb[3] H31c (a' = 3a, b' = 3b) (P3c1, 158); [3] R3c (a' = a - b, b' = a + 2b, c' = 3c) (161); [3] R3c (a' = 2a + b, b' = -a + b, c' = 3c) (161)

Maximal isomorphic subgroups of lowest index

IIc[3] P31c (c' = 3c) (159); [4] P31c (a' = 2a, b' = 2b) (159)

Minimal non-isomorphic supergroups

I[2] P-31c (163); [2] P6cc (184); [2] P63mc (186); [2] P-62c (190)
II[3] H31c (P3c1, 158); [2] P31m (c' = 1/2c) (157)








































to end of page
to top of page