| | | Special: as above, plus
|
| | x, 0, z | 0, x, z | -x, -x, z | -x, 0, z + 1/2 | | 0, -x, z + 1/2 | x, x, z + 1/2 | 0, x, -z + 1/2 | x, 0, -z + 1/2 | | -x, -x, -z + 1/2 | 0, -x, -z | -x, 0, -z | x, x, -z |
| no extra conditions |
| | x, y, 1/4 | -y, x - y, 1/4 | -x + y, -x, 1/4 | -x, -y, 3/4 | y, -x + y, 3/4 | x - y, x, 3/4 | | y, x, 1/4 | x - y, -y, 1/4 | -x, -x + y, 1/4 | -y, -x, 3/4 | -x + y, y, 3/4 | x, x - y, 3/4 |
| no extra conditions |
| | x, 2x, 0 | (-2x), -x, 0 | x, -x, 0 | -x, (-2x), 1/2 | 2x, x, 1/2 | -x, x, 1/2 | | -x, (-2x), 0 | 2x, x, 0 | -x, x, 0 | x, 2x, 1/2 | (-2x), -x, 1/2 | x, -x, 1/2 |
| hkil : l = 2n
|
| | 1/3, 2/3, z | 2/3, 1/3, z + 1/2 | 2/3, 1/3, -z + 1/2 | 1/3, 2/3, -z | | 2/3, 1/3, -z | 1/3, 2/3, -z + 1/2 | 1/3, 2/3, z + 1/2 | 2/3, 1/3, z |
| hkil : l = 2n
|
| | x, 0, 1/4 | 0, x, 1/4 | -x, -x, 1/4 | -x, 0, 3/4 | 0, -x, 3/4 | x, x, 3/4 |
| no extra conditions |
| | 1/2, 0, 0 | 0, 1/2, 0 | 1/2, 1/2, 0 | 1/2, 0, 1/2 | 0, 1/2, 1/2 | 1/2, 1/2, 1/2 |
| hkil : l = 2n
|
| | 0, 0, z | 0, 0, z + 1/2 | 0, 0, -z + 1/2 | 0, 0, -z |
| hkil : l = 2n
|
| | 1/3, 2/3, 0 | 2/3, 1/3, 1/2 | 2/3, 1/3, 0 | 1/3, 2/3, 1/2 |
| hkil : l = 2n
|
| | 1/3, 2/3, 1/4 | 2/3, 1/3, 3/4 | 2/3, 1/3, 1/4 | 1/3, 2/3, 3/4 |
| hkil : l = 2n
|
| | hkil : l = 2n
|
| | hkil : l = 2n
|
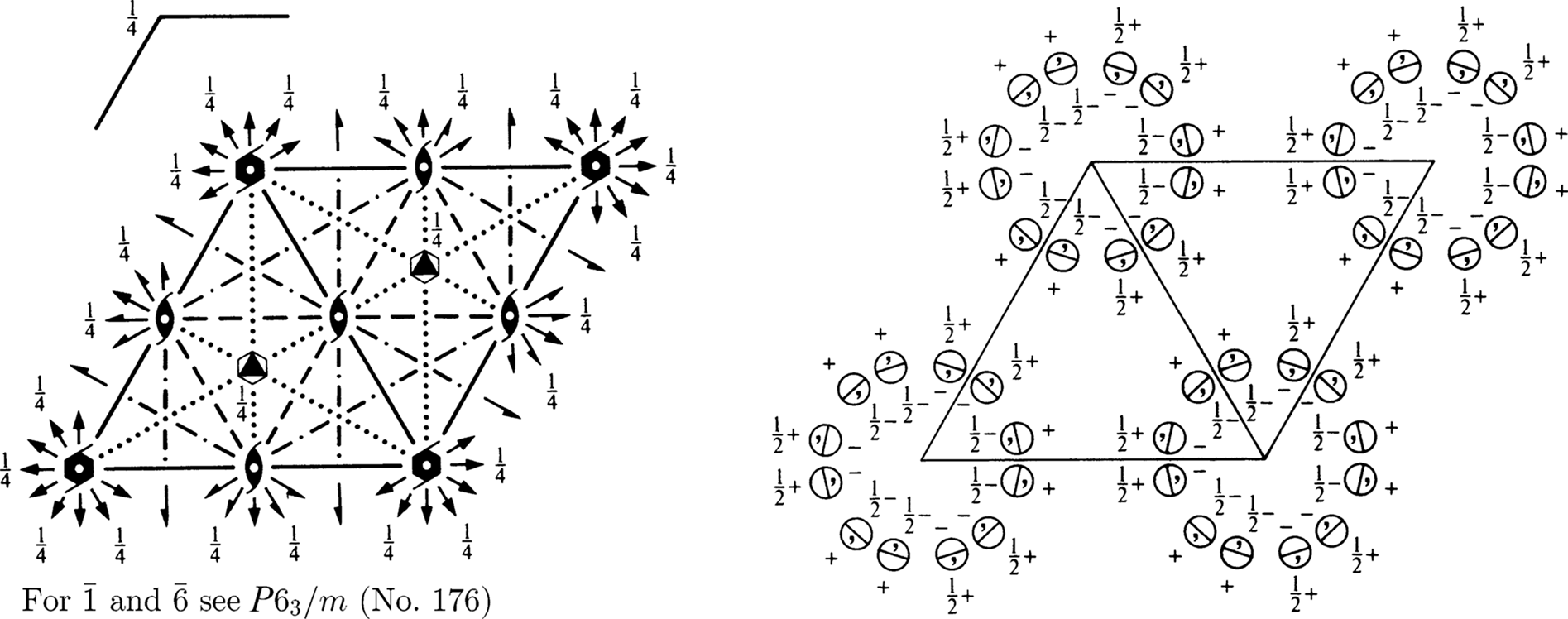

![[brace]](/graphics/sg/brace3.gif)

