|
International
Tables for Crystallography Volume I X-ray absorption spectroscopy and related techniques Edited by C. T. Chantler, F. Boscherini and B. Bunker |
Open
 access access
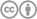
International Tables for Crystallography (2022). Vol. I. Early view chapter
https://doi.org/10.1107/S157487072200163X Magnetic X-ray techniques
a
Diamond Light Source, Harwell Science and Innovation Campus, Didcot OX11 0DE, United Kingdom The underlying theoretical aspects of X-ray spectroscopies are recapitulated with special emphasis on applications to magnetic systems. Prominence is placed on common conceptual aspects, while highlighting the differences in information that they may offer. X-ray scattering can be used to investigate the electronic and magnetic long-range order in crystals and ordered materials. The crystal symmetry of the sample and the X-ray polarization state have a profound effect on the scattering amplitude of X-ray resonant magnetic scattering (XRMS). Expressions for X-ray magnetic circular and linear dichroism (XMCD and XMLD, respectively) can be derived directly from those for XRMS. The photon–matter interaction for electric and magnetic multipole fields is presented from a general point of view, which reveals the physical implications of the various terms in the cross section for X-ray absorption. X-ray optical activity is due to mixed terms of different multipole rank of the electric and magnetic fields. The different optical effects, such as XMCD, X-ray natural circular dichroism (XNCD) and X-ray magnetic chiral dichroism (XMχD), can be distinguished by their properties under space inversion and time reversal. Keywords: magnetism; sum rules; spin and orbital moments. |
The theoretical concepts behind magnetic synchrotron techniques are based on quantum mechanics and provide very rich grounds for experimental exploration. The aim of this chapter is to present a general framework that shows the current and future capabilities, although many details are skipped due to page-length considerations. We will first present the general expressions for the scattering amplitude in nonresonant and resonant elastic scattering. From this, expressions for X-ray magnetic circular and linear dichroism (XMCD and XMLD, respectively) are obtained using the optical theorem. Taking crystal-field interaction into account leads to a remarkable result for XMLD.
The advantage of X-ray resonant magnetic scattering (XRMS), compared with other absorption spectroscopies, is that the scattering amplitudes from the various sites interfere coherently, which gives a sensitivity to long-range order. XRMS allows us to investigate the physics of higher order multipoles for the study of strongly correlated electron systems.
We review the interaction of electric and magnetic multipole fields with matter and explain the origin of X-ray optical activity.
The first magnetic scattering experiment was carried out on NiO under nonresonant conditions (de Bergevin & Brunel, 1981![[link]](/graphics/greenarr.gif) ). Subsequent magnetic scattering at resonance (Hannon et al., 1988
). Subsequent magnetic scattering at resonance (Hannon et al., 1988![[link]](/graphics/greenarr.gif) ) showed an enhancement of several orders of magnitude in the scattering amplitude, and also showed a strong dependence on the polarization state of the incident and scattered X-rays. This can be formally taken into account by describing the atomic scattering amplitude as a tensor quantity, instead of a scalar, with consequences for the selection rules of the diffracted intensity. The tensor products associated with the scattering amplitude must belong to the totally symmetric representation of the point group at the resonating ion.
) showed an enhancement of several orders of magnitude in the scattering amplitude, and also showed a strong dependence on the polarization state of the incident and scattered X-rays. This can be formally taken into account by describing the atomic scattering amplitude as a tensor quantity, instead of a scalar, with consequences for the selection rules of the diffracted intensity. The tensor products associated with the scattering amplitude must belong to the totally symmetric representation of the point group at the resonating ion.
In the scattering process, the incident and scattered photons are characterized by wavevectors k and k′, unit polarization vectors ɛ and ɛ′ and energies ℏωk and , respectively. Initially, the electrons are in the ground state |g〉 with energy Eg. Within the first Born approximation the differential cross section for coherent elastic X-ray scattering (
) is
where r0 = e2/mc2 is the classical electron radius, fj is the scattering amplitude of the electron at lattice position rj and q = k − k′ is the scattering vector.
Using the photon–matter interaction Hamiltonian (see also Section 2 of van der Laan & Figueroa, 2022
![[link]](/graphics/greenarr.gif) ) the scattering amplitude in the Kramers–Heisenberg formalism can be written as (Sakurai, 1985
) the scattering amplitude in the Kramers–Heisenberg formalism can be written as (Sakurai, 1985![[link]](/graphics/greenarr.gif) ; Blume, 1985
; Blume, 1985![[link]](/graphics/greenarr.gif) )
) with the scattering tensor
where pj and sj are the momentum operator and the spin at site j, respectively. Substituting into
the magnetic field H = −ik × A with vector potential A = ɛexp(ik · r), and using s · (k × ɛ) = (k × s) · ɛ, the current operator can be written as
, which reduces to
for electric dipole transitions.
The first term in equation (3![[link]](/graphics/greenarr.gif) ) gives the Thomson scattering amplitude f0 originating from the isotropic charge-density distribution. It also gives incoherent processes, such as nonresonant inelastic scattering (NIXS) and Compton scattering. The magnetic Compton profile, which can be measured with high-energy circularly polarized X-rays (100–200 keV), corresponds to the difference in the one-dimensional projection of the spin-polarized electron momentum density for majority and minority spin bands.
) gives the Thomson scattering amplitude f0 originating from the isotropic charge-density distribution. It also gives incoherent processes, such as nonresonant inelastic scattering (NIXS) and Compton scattering. The magnetic Compton profile, which can be measured with high-energy circularly polarized X-rays (100–200 keV), corresponds to the difference in the one-dimensional projection of the spin-polarized electron momentum density for majority and minority spin bands.
The second term in equation (3![[link]](/graphics/greenarr.gif) ) gives the nonresonant X-ray magnetic scattering amplitude, which is due to the orbital and spin magnetic density contributions. The vectors a and b contain the coupling between the photon polarization and the scattering vectors. The third term, also known as the anomalous or dispersive term, gives the resonant amplitude, fXRMS = f′ − if′′, arising from the core–valence transitions. fXRMS probes the intermediate states |n〉 with energy En, selected at the photon energy ℏω = En − Eg with a full width Γn for the lifetime. The intermediate state in the resonance process enables additional excitation paths that are otherwise not allowed in the direct transition, such as spin-flip transitions and forbidden transitions (see Section 2.3
) gives the nonresonant X-ray magnetic scattering amplitude, which is due to the orbital and spin magnetic density contributions. The vectors a and b contain the coupling between the photon polarization and the scattering vectors. The third term, also known as the anomalous or dispersive term, gives the resonant amplitude, fXRMS = f′ − if′′, arising from the core–valence transitions. fXRMS probes the intermediate states |n〉 with energy En, selected at the photon energy ℏω = En − Eg with a full width Γn for the lifetime. The intermediate state in the resonance process enables additional excitation paths that are otherwise not allowed in the direct transition, such as spin-flip transitions and forbidden transitions (see Section 2.3![[link]](/graphics/greenarr.gif) ). The resonance term can be ascribed to virtual transitions of an electron from a core state to an unoccupied state above the Fermi level. This is schematically illustrated in Fig. 1
). The resonance term can be ascribed to virtual transitions of an electron from a core state to an unoccupied state above the Fermi level. This is schematically illustrated in Fig. 1![[link]](/graphics/greenarr.gif) (a) for the soft X-ray excitation 3dn → 2p53dn+1 → 3dn in a magnetic transition-metal ion.
(a) for the soft X-ray excitation 3dn → 2p53dn+1 → 3dn in a magnetic transition-metal ion.
In contrast to absorption spectroscopies such as X-ray absorption spectroscopy (XAS) and resonant inelastic X-ray scattering (RIXS), in XRMS the scattering amplitudes from the various sites interfere coherently, which gives a sensitivity to long-range structural, magnetic and multipolar order.
The most important absorption edges for hard XRMS cover the energy range 3.5–15 keV, which includes the 3d metal K edges, rare-earth L edges and actinide L edges, with scattering amplitudes of ∼0.01–0.1r0. In the soft X-ray region there is a huge enhancement of the resonant amplitude of ∼100r0 for 3d metal L edges and rare-earth M edges. However, in order to fulfil the scattering condition the X-ray wavelength must be shorter than two times the lattice periodicity of the crystalline ordered magnetic structure. The resonant magnetic scattering can be distinguished from the Thomson scattering by tuning on and off the resonance energy.
The next task at hand is to separate the resonant amplitude into the geometric and dynamic factors. We will show this for the electric 2L-pole resonance (EL) in spherical symmetry with current operator . The transition operator exp(ik · rj) can be expanded in a sum over scalar products of spherical multipole tensors
of rank k and components κ = −k, …, k as
where jk(qr) is the kth-order spherical Bessel function.
We will make use of the standard notation for the tensor product of two spherical tensors A(k) and (Varshalovich et al., 1988
![[link]](/graphics/greenarr.gif) ),
), which defines a spherical tensor of rank K and projection Q, using Clebsch–Gordan coefficients 〈kk′κκ′|KQ〉. Using this recoupling, the matrix elements for A · pj = (ɛ · pj)exp(ik · rj) can be written as a sum of products of a geometric and physical (dynamic) part
where the current operator,
in the physical part excites an electron from an occupied (core) to an empty (valence) state.
For the electric 2L-pole scattering factor we then obtain the multipole expansion (Luo et al., 1993![[link]](/graphics/greenarr.gif) ; Carra & Thole, 1994
; Carra & Thole, 1994![[link]](/graphics/greenarr.gif) )
) with physical part
and geometric part
For the electric–dipole resonance the dependence disappears and equation (8
![[link]](/graphics/greenarr.gif) ) reduces to
) reduces to containing a scalar F(0), a pseudovector (antisymmetric tensor) F(1) and a symmetric tensor F(2).
In uniaxial symmetry, with M along the axis, this leads to the Hannon & Trammel formula (Hannon et al., 1988
![[link]](/graphics/greenarr.gif) )
) F(0) gives the charge scattering
. F(1) gives the magnetic scattering
, which depends linearly on the magnetization direction and at resonance can become comparable in size to F(0). As an example, Figs. 1
![[link]](/graphics/greenarr.gif) (b) and 1
(b) and 1![[link]](/graphics/greenarr.gif) (c) shows the charge (
(c) shows the charge ( and
) and magnetic (
and
) scattering at the Fe L2,3 edge of metallic iron. F(2) is quadratic in the magnetization direction and is usually much smaller than F(0) and F(1). The resonant amplitudes are complex numbers with strongly energy-dependent phase angles. The real and imaginary parts are related to each other by a Kramers–Kronig transform.
The q-dependent scattering intensity is obtained by taking the modulus square of f(ɛ′, ɛ, ω), which gives the charge scattering, the pure magnetic scattering and the interference term between charge and magnetic scattering (van der Laan, 2008![[link]](/graphics/greenarr.gif) ). For instance, the intensity of the pure magnetic scattering in SO2 symmetry is
). For instance, the intensity of the pure magnetic scattering in SO2 symmetry is where Pσ = P0 + P1, Pπ = P0 − P1, P2 and P3 represent the Poincaré–Stokes parameters. The equation can be used to determine the polarization dependence of the vector magnetization profile for magnetic multilayers, domain structures, nano-objects, spiral and helical structures, skyrmions etc. (Zhang et al., 2017
![[link]](/graphics/greenarr.gif) ).
).
For a collinear structure with all of the magnetization vectors parallel, it follows from equation (1![[link]](/graphics/greenarr.gif) ) that the polarization dependence of the coherent scattering is the same as for the single site. This leads to an overlap of the magnetic and charge peaks; therefore, to study ferromagnetic materials the interference between these two contributions has to be used, which shows a change in the scattering signal upon reversal of the sample magnetization. Antiferromagnetically coupled layers and domains as well as spiral structures offer the advantage that the magnetic diffraction peaks are separated from the structural diffraction peaks. Doubling the periodicity in real space gives rise to magnetic peaks with half the structural period in reciprocal space.
) that the polarization dependence of the coherent scattering is the same as for the single site. This leads to an overlap of the magnetic and charge peaks; therefore, to study ferromagnetic materials the interference between these two contributions has to be used, which shows a change in the scattering signal upon reversal of the sample magnetization. Antiferromagnetically coupled layers and domains as well as spiral structures offer the advantage that the magnetic diffraction peaks are separated from the structural diffraction peaks. Doubling the periodicity in real space gives rise to magnetic peaks with half the structural period in reciprocal space.
The tensorial character of the scattering amplitude allows us to observe otherwise forbidden reflections, for which the crystal structure factor vanishes. The diffracted amplitude generated by the whole crystal is , where j runs over all sites. Thus, a necessary condition for reflection is that the total phase factor in the diffracted amplitude does not cancel. If all sites have the same f then we have
, which is the result for normal Bragg scattering. This situation changes when the various sites have different orientations (Carra & Thole, 1994
![[link]](/graphics/greenarr.gif) ). The components of the spherical tensor
). The components of the spherical tensor transform under space rotation like spherical harmonics with φ dependence exp(iζφ). An angular rotation of the spherical tensor by 2π/n gives a phase shift exp(2πiζ/n) and thus a scattering factor
. Screw axes and glide planes can give constructive interference. For instance, when q is along an n-fold screw axis parallel to c (i.e. with rotation 2π/n and translation tc/n), the spherical harmonics change by a factor exp(2πiζ/n) and the Bragg factor exp(iq · R) changes by a phase shift exp(iq · ct/n). Since this factor must reduce to unity, the reflection is only allowed when q · c/2π = (nk − ζ)/t, where k is an integer.
The Hannon and Trammel equation (equation 12![[link]](/graphics/greenarr.gif) ), which has successfully been used in a variety of studies, is restricted to cylindrical symmetry. It does not include crystal-field effects, which become important in localized materials such as oxides. To take these effects into account we have to branch down to the symmetry states of the excited sites. The tensor components in crystal-field symmetry can be obtained using the basis-state transformation
), which has successfully been used in a variety of studies, is restricted to cylindrical symmetry. It does not include crystal-field effects, which become important in localized materials such as oxides. To take these effects into account we have to branch down to the symmetry states of the excited sites. The tensor components in crystal-field symmetry can be obtained using the basis-state transformation , where Γ are the irreps of the point group. However, if M or ɛ are not along the symmetry directions of the point group then the symmetry of the total system reduces to the trivial group C1.
Alternatively, we can use the Cartesian tensor form. For instance, in cubic crystal-field symmetry (Oh) the scalar F(0) has the total symmetric irrep A1 = {1}, the pseudovector F(1) has the irrep T1 = {x, y, z} and the symmetric tensor F(2) has the irreps E = {, x2 − y2} and T2 = {xy, yz, zx}. Thus, the diagonal matrix elements contain
and
, while the nondiagonal elements contain
and
with a corresponding symmetry of the magnetization.
Taking , with unit magnetization vector
=
and polarization vector ɛ = (ɛx, ɛy, ɛz), the scattering tensor
along
can be written as (Haverkort et al., 2010
![[link]](/graphics/greenarr.gif) ; van der Laan, 2013a
; van der Laan, 2013a![[link]](/graphics/greenarr.gif) )
) To include the third-rank tensor
, the elements of which are usually small, we can append it to the odd-rank tensor
by the substitution
The absorption cross section is obtained by the optical theorem as the imaginary part of the scattering amplitude F in forward direction, Thus, the expressions for X-ray absorption are obtained by taking ɛ′ = ɛ in those for the scattering amplitude.
As an example, we give here the scattering amplitude for XMCD in orthorhombic symmetry (D2h). The tensor F(1) has elements with irreps B1 = {z}, B2 = {y} and B3 = {x}, which gives a directional dependence of with respect to the crystal frame. The Cartesian scattering tensor along
is
where in the right-hand side the antisymmetric tensor is converted by index contraction [
with Levi–Civita symbol ɛijk] into an axial vector. Then,
, where P = −i(ɛ* × ɛ) is the helicity vector.
The spin and orbital sum rules for XMCD are treated in van der Laan (2022![[link]](/graphics/greenarr.gif) ) and the angular dependence of XMCD in van der Laan & Figueroa (2022
) and the angular dependence of XMCD in van der Laan & Figueroa (2022![[link]](/graphics/greenarr.gif) ). XMCD has become a workhorse technique in physics and materials science with vast applications, and reviews can be found in, for example, Stöhr & Siegmann (2006
). XMCD has become a workhorse technique in physics and materials science with vast applications, and reviews can be found in, for example, Stöhr & Siegmann (2006![[link]](/graphics/greenarr.gif) ), van der Laan (2013b
), van der Laan (2013b![[link]](/graphics/greenarr.gif) ) and van der Laan & Figueroa (2014
) and van der Laan & Figueroa (2014![[link]](/graphics/greenarr.gif) ).
).
For cubic crystal-field symmetry the scattering tensor , given in equation (14
![[link]](/graphics/greenarr.gif) ), has diagonal elements with irrep E and nondiagonal elements with irrep T2, so that the XMLD depends on the directions of ɛ and
), has diagonal elements with irrep E and nondiagonal elements with irrep T2, so that the XMLD depends on the directions of ɛ and with respect to the crystal frame.
For arbitrary directions of ɛ and in cubic crystal-field symmetry the XMLD is a linear combination of two fundamental spectra, which are related to the threefold and fourfold symmetry axes (Arenholz et al., 2006
![[link]](/graphics/greenarr.gif) ). In this case, the XMLD can be separated into an isotropic and an anisotropic part. The isotropic part is proportional to
). In this case, the XMLD can be separated into an isotropic and an anisotropic part. The isotropic part is proportional to , which depends only on the included angle and is therefore rotationally invariant. The anisotropic part contains the dependence on the ɛ and
directions with respect to the crystal axes. It vanishes in the absence of a crystal field. Notably, there is the curious case of the Ni2+ L2 edge, where the XMLD only has an anisotropic part, and the
and
spectra have the same shape but opposite sign. Further details can be found in Haverkort et al. (2010
![[link]](/graphics/greenarr.gif) ) and van der Laan (2013a
) and van der Laan (2013a![[link]](/graphics/greenarr.gif) ).
).
In symmetries lower than cubic, there are two distinctly different ways to obtain the XMLD, i.e., by rotating the orientation of either the linear polarization or the magnetization, which give the charge or the magnetic anisotropy, respectively.
X-ray optical activity arises from the interference between different terms in the multipole expansion of the electromagnetic field. We will follow the derivation of Rose & Brink (1967![[link]](/graphics/greenarr.gif) ) and van der Laan (2006
) and van der Laan (2006![[link]](/graphics/greenarr.gif) ) and present relevant results.
) and present relevant results.
The Hamiltonian of a single particle in the presence of a classic electromagnetic field is where e is the charge and
is the spin magnetic moment of the particle, β = eℏ/2mc is the Bohr magneton, A and φ are the vector and scalar electromagnetic potential, respectively, and r is the electron position vector. In the following we will use natural units ℏ = 1. The gauge condition is taken such that φ = 0 and we neglect the two-photon process given by the A2 term. This leads to a kinetic energy term
and an interaction Hamiltonian comprising a charge and spin term,
where gl and gs are the orbital and spin g-factors. The aim is to expand the transverse plane wave A in a series of spherical vector fields
and
, thereby expressing the interaction Hamiltonian in a series of tensor operators
and
, which are the products of momentum p and spin S with the fields
and
.
We define the electric and magnetic multipole fields where the scalar functions
satisfy the wave equation ∇2Φ + k2Φ = 0 and form a complete set.
The expansion for circularly polarized vector plane waves with component q = 1 (right-handed) and q = −1 (left-handed) can be written as where
is the rotation matrix that takes the z axis into the direction of the vector k, and the index π in the compact expression runs over E (π = 0) and M (π = 1). The polarization vectors are defined as ɛ±1 = ∓(ɛx + iɛy)/(2)1/2 and ɛ0 = ɛz are co(ntra)variant components:
.
In the long-wavelength approximation, kr ≪ 1, the spherical Bessel functions obtain the approximate value jL(kr) ≈ (kr)L/(2L + 1)!!, so that the scalar potential ΦLM takes the simplified form ΦLM = rLCLM(ik)L/(2L − 1)!!. This gives for the interaction Hamiltonian The charge and spin interactions of the electric and magnetic multipole fields result in a total of four terms in the interaction Hamiltonian,
with the electric (Q) and magnetic (M) multipole operators
where the unprimed and primed operators result from the charge and spin interactions, respectively. The Hamiltonian can be cast in a simplified form using the interaction multipole operators
, with π = 0 for E and π = 1 for M, which are sets of operators all having the same transformation properties,
Specifically, for the prefactor we have
,
and
. We have the parity rules PΦLM = (−)LΦLM,
and
. The parity of AE · p and S · (∇ × AE) is (−)L, whereas the parity of AM · p and S · (∇ × AM) is (−)L+1. Therefore, the electric and magnetic 2L-pole interaction operators
connect states that differ in parity by a factor (−)L+π. Thus E1 has odd parity, while M1 and E2 have even parity.
Using the expansion for the exponential we can separate A · p =
into the geometric and dynamic factors given in Table 1
![[link]](/graphics/greenarr.gif) , using the tensor product notation defined in equation (5
, using the tensor product notation defined in equation (5![[link]](/graphics/greenarr.gif) ). The prefactor
). The prefactor is given in equation (27
![[link]](/graphics/greenarr.gif) ). The different orders n in the expansion are alternatingly imaginary and real. The parity operator gives P(i, ɛ, k, p, r) = (i, −ɛ, −k, −p, −r). The time-reversal operator gives θ(i, ɛ, k, p, r) = (−i, ɛ*, −k, −p, r), hence the part iL+1kLp of the interaction operator
). The different orders n in the expansion are alternatingly imaginary and real. The parity operator gives P(i, ɛ, k, p, r) = (i, −ɛ, −k, −p, −r). The time-reversal operator gives θ(i, ɛ, k, p, r) = (−i, ɛ*, −k, −p, r), hence the part iL+1kLp of the interaction operator is always time-reversal even.
|
The zeroth-order contribution (n = 0) gives the E1 term ɛ · p ∝ iωɛ · r. The geometric factor ɛ is parity-odd.
The first-order contribution (n = 1) can be factorized into a geometric factor [ɛ, k](L) and a dynamic factor [p, r](L), which are both parity-even. For L = 0, the geometric factor vanishes due to transversality, i.e. ɛ · k = 0. The L = 1 term gives the magnetic dipole contribution (M1) with a geometric factor [ɛ, k](1) ∝ (k × ɛ) and a dynamic factor [p, r](1) ∝ (p × r) ∝ L. The L = 2 term yields the electric quadrupole contribution (E2) with a dynamic factor [p, r](2) ∝ L2 ∝ the charge quadrupole.
Thus, the leading terms in the transition amplitude can be written as where the first, second and third terms represent the electric dipole (E1), electric quadrupole (E2) and magnetic dipole (M1) transition amplitudes, respectively. The transition probability of E1 is much larger than those of E2 and M1. The M1 operator, with the monopole selection rules ΔJ ≤ 1, ΔL = 0, ΔS = 0 and Δn = 0, does not contain a radial variable; therefore, its matrix element vanishes if the radial parts of the initial and final states are orthogonal. The M1 transition occurs only at low excitation energies and can be neglected in core-level spectroscopy, since it requires configuration interaction. The explicit angular dependence of the E1 and E2 transitions can be found in Brouder (1990
![[link]](/graphics/greenarr.gif) ).
).
According to Fermi's golden rule in quantum mechanics, the absorption cross section σ(ω) is given by the matrix element product of the interaction between the initial and the final state, summed over final states with the same energy, which contains interference terms such as E1M1 and E1E2.
The ELEL′ absorption cross section can be written as where the tensors
and
give the geometric and dynamic factor, respectively, of rank b and time-reversal phase factor (−)τ. For the squared matrix elements in equation (30
![[link]](/graphics/greenarr.gif) ) the geometric factor (c.f. Table 1
) the geometric factor (c.f. Table 1![[link]](/graphics/greenarr.gif) )
) with parity condition
. The time-reversal symmetry can be even (τ = 0) or odd (τ = 1). As
in equation (32
![[link]](/graphics/greenarr.gif) ) does not have a well defined behaviour under time reversal, we recouple it to the form
) does not have a well defined behaviour under time reversal, we recouple it to the form where N = L + L′ − 2 is the number of times that k appears in the geometric factor. The tensor X has the triangle condition, |N − a| ≤ b ≤ N + a. The parity condition is (−)Π = (−)N. The time-reversal condition is
For a = 0, we have ɛ* · ɛ = 1 and the geometric factor k(N) is polarization-independent, so that we obtain (−)τ = (−)b = (−)N = (−)Π. Thus, these indices must be either all even or all odd. An even value corresponds to the normal spectrum, while an odd value corresponds to the XMχD.
For a = 1, we have (ɛ* × ɛ) ∝ ik. This gives a chiral effect, defined as one in which the intensity contribution is reversed by conjugating the polarization vectors (Stedman, 1990![[link]](/graphics/greenarr.gif) ). Since k × k(N) = 0 we have b = N ± 1, and using (−)τ = (−)N+1 we obtain b + τ is even. Equation (34
). Since k × k(N) = 0 we have b = N ± 1, and using (−)τ = (−)N+1 we obtain b + τ is even. Equation (34![[link]](/graphics/greenarr.gif) ) leads to two different possibilities for the chiral effect. The first is Π = 0 and τ = 1, which gives magnetic circular dichroism (MCD) with b odd and N even. The second possibility is Π = 1 and τ = 0, which gives the natural circular dichroism (NCD) with b even and N odd (c.f. Table 2
) leads to two different possibilities for the chiral effect. The first is Π = 0 and τ = 1, which gives magnetic circular dichroism (MCD) with b odd and N even. The second possibility is Π = 1 and τ = 0, which gives the natural circular dichroism (NCD) with b even and N odd (c.f. Table 2![[link]](/graphics/greenarr.gif) ).
).
|
For a = 2 we have (−)τ = (−)Π = (−)N, while b can have different values. b = 1 contributes to the XMχD and b = 2 and b = 3 contribute to the XMLD.
In the case that L = L′, the parity is even so that (−)τ = (−)a, hence τ is even and odd for even and odd a, respectively. In the special case N = 0 (i.e. E1E1) we have T(b, τ) = [ɛ*, ɛ](a), hence a = b. For the isotropic spectrum (a = 0) the sum rule gives the number of particles n (Thole & van der Laan, 1988![[link]](/graphics/greenarr.gif) ). For the X-ray magnetic circular dichroism (XMCD; a = 1) the sum rule gives the orbital moment L (Thole et al., 1992
). For the X-ray magnetic circular dichroism (XMCD; a = 1) the sum rule gives the orbital moment L (Thole et al., 1992![[link]](/graphics/greenarr.gif) ). For the X-ray magnetic linear dichroism (XMLD; a = 2) the sum rule gives the quadrupole moment Q ∝ L2 (Carra et al., 1993
). For the X-ray magnetic linear dichroism (XMLD; a = 2) the sum rule gives the quadrupole moment Q ∝ L2 (Carra et al., 1993![[link]](/graphics/greenarr.gif) ; van der Laan, 1999
; van der Laan, 1999![[link]](/graphics/greenarr.gif) ).
).
All interference terms have N odd, so that (−)τ = (−)a+1, i.e. τ + a is odd, hence τ is even and odd for odd and even a, respectively.
The effective operators which form the sum-rule results can be built from the triad of mutually orthogonal vector operators (Goulon et al., 2003![[link]](/graphics/greenarr.gif) ; Carra et al., 2003
; Carra et al., 2003![[link]](/graphics/greenarr.gif) ): n = r/r, which is a time-even, polar vector, typically associated with the electric dipole moment, the orbital angular momentum L, which is a time-odd, axial vector, and the toroidal vector Ω = ½[(n × L) − (L × n)] = ½i[n, L2], which is odd with respect to both inversion and time reversal and is proportional to the orbital anapole moment.
): n = r/r, which is a time-even, polar vector, typically associated with the electric dipole moment, the orbital angular momentum L, which is a time-odd, axial vector, and the toroidal vector Ω = ½[(n × L) − (L × n)] = ½i[n, L2], which is odd with respect to both inversion and time reversal and is proportional to the orbital anapole moment.
The E1E2 interference has a geometric factor =
and the multipole selection rules impose a mixing (hybridization) between l and l + 1 valence levels. The following results have been reported (Goulon et al., 2003
![[link]](/graphics/greenarr.gif) ; Carra et al., 2003
; Carra et al., 2003![[link]](/graphics/greenarr.gif) ).
).
The X-ray magnetochiral dichroism (XMχD) sum rule involves the ground-state expectation value of the toroidal vector Ω(1,τ=1) with a geometric factor , associated with the Stokes component S0.
The XNCD sum rule gives the expectation value of the time-even pseudodeviator N(2,τ=0) = [L, Ω](2) and T(2,τ=0) = .
For the nonreciprocal XMLD the effective operator must be a time-odd pseudodeviator and
.
An effective operator Γ(3,τ=1) = [[L, L](2), Ω](3) is involved in the sum rules for both XMχD and nonreciprocal XMLD.
The results in Section 3.2![[link]](/graphics/greenarr.gif) permit a simple physical description of the optical effects. Pure transitions must have even parity. The only way of inducing natural (field-independent) optical activity is by interference between multipoles of different order in the k-expansion of the photon wavevector. Only the interference of a real and an imaginary term
permit a simple physical description of the optical effects. Pure transitions must have even parity. The only way of inducing natural (field-independent) optical activity is by interference between multipoles of different order in the k-expansion of the photon wavevector. Only the interference of a real and an imaginary term can lead to odd parity. The E1M1 interference in the visible region allows the detection of natural circular dichroism and optical rotation, such as in the well known example of a sugar solution. Although in the visible region the E2 transitions are negligibly small, their magnitude increases with photon energy, so that for harder X-rays the E1E2 interference can be observed. We can distinguish the different optical effects by their properties under space inversion and time reversal, as given in Table 2
![[link]](/graphics/greenarr.gif) .
.
As a general rule, dichroism can only exist if there is no symmetry that reverses only one measurable observable but leaves the rest of the system unchanged. In the Faraday effect the time-reversal operator reverses both the magnetization and the direction of the light, thereby leaving the total physical system invariant. In natural circular dichroism, the parity operator reverses the rotation angle (screw sense) of both the medium and the light, again leaving the total system invariant. Nonzero effects only show up in crystals that have the appropriate symmetry class. Nonreciprocal optical effects invoke magnetic moments, since they are time non-invariant. They are characterized by a reversal of the phase rotation when the light propagates in the opposite direction, such as in the Faraday rotation in transmission or the Kerr effect in reflection. Magnetic circular dichroism (MCD), the difference in absorption for left- and right-circularly polarized light in the presence of an external magnetic field, also belongs to this category. Nonreciprocal optical effects are not restricted to media that possess a net magnetic moment, such as ferromagnets and ferrimagnets. Magnetoelectric antiferromagnets belong to the special class of magnetic ordered materials where there is no net magnetic moment but, in addition to time reversal, the parity symmetry is also broken, while the combined symmetry operation is conserved. Goulon et al. (2000![[link]](/graphics/greenarr.gif) ) reported a nonreciprocal transverse anisotropy in the low-temperature antiferromagnetic insulating phase of a chromium-doped V2O3 crystal in which one single antiferromagnetic domain was grown by magnetoelectric annealing.
) reported a nonreciprocal transverse anisotropy in the low-temperature antiferromagnetic insulating phase of a chromium-doped V2O3 crystal in which one single antiferromagnetic domain was grown by magnetoelectric annealing.
Here, we show how to distinguish experimentally between the different optical effects. Reversing the photon helicity vector λ and the magnetization M gives the spectra shown in Table 3![[link]](/graphics/greenarr.gif) , where the superscripts + and − indicate an alignment along the positive and negative direction. These spectra are symmetric (even) or antisymmetric (odd) in λ and M. Note the difference between this table, where the parity comes from the helicity vector, and Table 2
, where the superscripts + and − indicate an alignment along the positive and negative direction. These spectra are symmetric (even) or antisymmetric (odd) in λ and M. Note the difference between this table, where the parity comes from the helicity vector, and Table 2![[link]](/graphics/greenarr.gif) , where even and odd parity is connected to pure and mixed multipole transitions, respectively.
, where even and odd parity is connected to pure and mixed multipole transitions, respectively.
|
By symmetry, the different spectra correspond to the irreducible representations of the point group D2 = C2 ⊗ C2, for which the character table is shown in Table 4![[link]](/graphics/greenarr.gif) . Even and odd functions are indicated by 1 and −1, respectively.
. Even and odd functions are indicated by 1 and −1, respectively.
|
Table 4![[link]](/graphics/greenarr.gif) shows that the XMCD is the difference between spectra with M and λ parallel and antiparallel, respectively. Therefore, it is odd in both λ and M, but even in M ⊗ λ. The XNCD is the difference between spectra with opposite λ and is independent of M. The XMχD is the difference between spectra with opposite M and is independent of λ; hence, it can be measured using linear polarization.
shows that the XMCD is the difference between spectra with M and λ parallel and antiparallel, respectively. Therefore, it is odd in both λ and M, but even in M ⊗ λ. The XNCD is the difference between spectra with opposite λ and is independent of M. The XMχD is the difference between spectra with opposite M and is independent of λ; hence, it can be measured using linear polarization.
References
 Arenholz, E., van der Laan, G., Chopdekar, R. V. & Suzuki, Y. (2006). Phys. Rev. B, 74, 094407.Google Scholar
Arenholz, E., van der Laan, G., Chopdekar, R. V. & Suzuki, Y. (2006). Phys. Rev. B, 74, 094407.Google Scholar Bergevin, F. de & Brunel, M. (1981). Acta Cryst. A37, 314–324.Google Scholar
Bergevin, F. de & Brunel, M. (1981). Acta Cryst. A37, 314–324.Google Scholar Blume, M. (1985). J. Appl. Phys. 57, 3615–3618.Google Scholar
Blume, M. (1985). J. Appl. Phys. 57, 3615–3618.Google Scholar Brouder, C. (1990). J. Phys. Condens. Matter, 2, 701–738.Google Scholar
Brouder, C. (1990). J. Phys. Condens. Matter, 2, 701–738.Google Scholar Carra, P., Jerez, A. & Marri, I. (2003). Phys. Rev. B, 67, 045111.Google Scholar
Carra, P., Jerez, A. & Marri, I. (2003). Phys. Rev. B, 67, 045111.Google Scholar Carra, P. & Thole, B. T. (1994). Rev. Mod. Phys. 66, 1509–1515.Google Scholar
Carra, P. & Thole, B. T. (1994). Rev. Mod. Phys. 66, 1509–1515.Google Scholar Carra, P., Thole, B. T., Altarelli, M. & Wang, X. (1993). Phys. Rev. Lett. 70, 694–697.Google Scholar
Carra, P., Thole, B. T., Altarelli, M. & Wang, X. (1993). Phys. Rev. Lett. 70, 694–697.Google Scholar Goulon, J., Rogalev, A., Goulon-Ginet, C., Benayoun, G., Paolasini, L., Brouder, C., Malgrange, C. & Metcalf, P. A. (2000). Phys. Rev. Lett. 85, 4385–4388.Google Scholar
Goulon, J., Rogalev, A., Goulon-Ginet, C., Benayoun, G., Paolasini, L., Brouder, C., Malgrange, C. & Metcalf, P. A. (2000). Phys. Rev. Lett. 85, 4385–4388.Google Scholar Goulon, J., Rogalev, A., Wilhelm, F., Goulon-Ginet, C., Carra, P., Marri, I. & Brouder, C. (2003). J. Exp. Theor. Phys. 97, 402–431.Google Scholar
Goulon, J., Rogalev, A., Wilhelm, F., Goulon-Ginet, C., Carra, P., Marri, I. & Brouder, C. (2003). J. Exp. Theor. Phys. 97, 402–431.Google Scholar Hannon, J. P., Trammell, G. T., Blume, M. & Gibbs, D. (1988). Phys. Rev. Lett. 61, 1245–1248.Google Scholar
Hannon, J. P., Trammell, G. T., Blume, M. & Gibbs, D. (1988). Phys. Rev. Lett. 61, 1245–1248.Google Scholar Haverkort, M. W., Hollmann, N., Krug, I. P. & Tanaka, A. (2010). Phys. Rev. B, 82, 094403.Google Scholar
Haverkort, M. W., Hollmann, N., Krug, I. P. & Tanaka, A. (2010). Phys. Rev. B, 82, 094403.Google Scholar Laan, G. van der (1999). Phys. Rev. Lett. 82, 640–643.Google Scholar
Laan, G. van der (1999). Phys. Rev. Lett. 82, 640–643.Google Scholar Laan, G. van der (2006). Magnetism: A Synchrotron Radiation Approach, Lecture Notes in Physics, Vol. 697, edited by E. Beaurepaire, H. Bulou, F. Scheurer & J.-P. Kappler, pp. 143–200. Heidelberg: Springer.Google Scholar
Laan, G. van der (2006). Magnetism: A Synchrotron Radiation Approach, Lecture Notes in Physics, Vol. 697, edited by E. Beaurepaire, H. Bulou, F. Scheurer & J.-P. Kappler, pp. 143–200. Heidelberg: Springer.Google Scholar Laan, G. van der (2008). C. R. Phys. 9, 570–584.Google Scholar
Laan, G. van der (2008). C. R. Phys. 9, 570–584.Google Scholar Laan, G. van der (2013a). Magnetism and Synchrotron Radiation: Towards the Fourth Generation Light Sources, Springer Proceedings in Physics, Vol. 151, edited by E. Beaurepaire, H. Bulou, L. Joly & F. Scheurer, pp. 239–256. Cham: Springer International.Google Scholar
Laan, G. van der (2013a). Magnetism and Synchrotron Radiation: Towards the Fourth Generation Light Sources, Springer Proceedings in Physics, Vol. 151, edited by E. Beaurepaire, H. Bulou, L. Joly & F. Scheurer, pp. 239–256. Cham: Springer International.Google Scholar Laan, G. van der (2013b). J. Phys. Conf. Ser. 430, 012127.Google Scholar
Laan, G. van der (2013b). J. Phys. Conf. Ser. 430, 012127.Google Scholar Laan, G. van der (2022). Int. Tables Crystallogr. I, https://doi.org/10.1107/S1574870722005390
.Google Scholar
Laan, G. van der (2022). Int. Tables Crystallogr. I, https://doi.org/10.1107/S1574870722005390
.Google Scholar Laan, G. van der & Figueroa, A. I. (2014). Coord. Chem. Rev. 277–278, 95–129.Google Scholar
Laan, G. van der & Figueroa, A. I. (2014). Coord. Chem. Rev. 277–278, 95–129.Google Scholar Laan, G. van der & Figueroa, A. I. (2022). Int. Tables Crystallogr. I, https://doi.org/10.1107/S1574870722001628
.Google Scholar
Laan, G. van der & Figueroa, A. I. (2022). Int. Tables Crystallogr. I, https://doi.org/10.1107/S1574870722001628
.Google Scholar Luo, J., Trammell, G. T. & Hannon, J. P. (1993). Phys. Rev. Lett. 71, 287–290.Google Scholar
Luo, J., Trammell, G. T. & Hannon, J. P. (1993). Phys. Rev. Lett. 71, 287–290.Google Scholar Rose, H. J. & Brink, D. M. (1967). Rev. Mod. Phys. 39, 306–347.Google Scholar
Rose, H. J. & Brink, D. M. (1967). Rev. Mod. Phys. 39, 306–347.Google Scholar Sakurai, J. J. (1985). Modern Quantum Mechanics. Redwood City: Addison-Wesley.Google Scholar
Sakurai, J. J. (1985). Modern Quantum Mechanics. Redwood City: Addison-Wesley.Google Scholar Stedman, G. E. (1990). Diagram Techniques in Group Theory. Cambridge University Press.Google Scholar
Stedman, G. E. (1990). Diagram Techniques in Group Theory. Cambridge University Press.Google Scholar Stöhr, J. & Siegmann, H. C. (2006). Magnetism: From Fundamentals to Nanoscale Dynamics. Berlin, Heidelberg: Springer.Google Scholar
Stöhr, J. & Siegmann, H. C. (2006). Magnetism: From Fundamentals to Nanoscale Dynamics. Berlin, Heidelberg: Springer.Google Scholar Thole, B. T., Carra, P., Sette, F. & van der Laan, G. (1992). Phys. Rev. Lett. 68, 1943–1946.Google Scholar
Thole, B. T., Carra, P., Sette, F. & van der Laan, G. (1992). Phys. Rev. Lett. 68, 1943–1946.Google Scholar Thole, B. T. & van der Laan, G. (1988). Phys. Rev. A, 38, 1943–1947.Google Scholar
Thole, B. T. & van der Laan, G. (1988). Phys. Rev. A, 38, 1943–1947.Google Scholar Varshalovich, D. A., Moskalev, A. N. & Khersonskii, V. K. (1988). Quantum Theory of Angular Momentum. Singapore: World Scientific.Google Scholar
Varshalovich, D. A., Moskalev, A. N. & Khersonskii, V. K. (1988). Quantum Theory of Angular Momentum. Singapore: World Scientific.Google Scholar Zhang, S. L., van der Laan, G. & Hesjedal, T. (2017). Nat. Commun. 8, 14619.Google Scholar
Zhang, S. L., van der Laan, G. & Hesjedal, T. (2017). Nat. Commun. 8, 14619.Google Scholar
![[Figure 1]](/figures/qy5023fig1thm.gif)

